特別講義DS Ch8 データの可視化
1 データの可視化
ここまでで,プログラミングを利用してデータを読み込み,編集ができるようになりました. これから,データを分析する手法を学習しましょう. データ分析の第一歩は,データの可視化です.
統計データはテーブル形式のまま,眺めても理解できません. データを可視化することで,データの特徴や意味を理解する助けになります. ここでは,データを可視化するいくつかの方法を学びましょう.
ライブラリのインストール
Pythonにおけるグラフ作成の,代表的なライブラリには,matplotlibやseabornがあります.
それぞれ, pip installしておきましょう.
matplotlib,seabornはそれぞれ以下のようにインポートするのが一般的です.
import matplotlib.pyplot as pltimport searborn as sns
matplotlibにおける日本語表示matplotlibは日本語などのマルチバイト文字に対応しておらず,日本語を使用すると日本語部分が日本語部分が, □(通称豆腐)に変わります.
例: 「Hello こんにちは」 → 「Hello □ □ □ □ □ 」
matplotlibで日本語を利用する方法として一番簡単なものに, japanize-matplotlibの利用があります.
pip install したあとに, import japanize_matplotlib をしましょう(pip では '-'(ハイフン)ですが,import文では,'_'(アンダーバー)なので注意してください.)
- Python 3.12 における
japanize_matplotlib
Python3.12では,japanize_matplotlibを読み込もうとすると,ModuleNotFoundError: No module named 'distutils' と表示されます.
これは,japanize_matplotlib内で利用されているdistutilsというモジュールが廃止されたことによります. こちらのエラーは, distutilsの代替であるsetuptoolsを pip installすることで消えます.
参考: 【inshellisense】ModuleNotFoundError: No module named ’distutils’の対処法
本章におけるコードは以下, 先頭に以下のような記述があることが前提となります.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns1.1 基礎的なグラフ(棒グラフ,円グラフ,折れ線グラフ)
matplotlibを利用して,グラフを作成する大まかな手順は以下のようになります.
データを準備する. BOMなしのCSVを作りましょう
pandasでプログラムでCSVを読み込みましょうグラフにしたい部分を抽出します.
グラフを作るために何が必要かはグラフの種類によります.
matplotlibのメソッドを利用してグラフを生成します.基本的なメソッドは以下のとおりです.
グラフの種類 メソッド 棒グラフ plt.bar(x軸のリスト,y軸のリスト)円グラフ plt.pie(カテゴリー別のデータのリスト,label=ラベル)折れ線グラフ plt.plot(x軸のリスト,y軸のリスト)散布図 plt.scatter(x軸のリスト,y軸のリスト)これら以外の,グラフに関しては個別に扱います.
グラフの見た目を整えます.
ある程度自動で設定されますが,色,メモリ,形,軸などを個別に設定できます.
グラフの要素 メソッド タイトル plt.title('タイトル')判例 plt.legend()y軸 plt.yticks(軸の目盛のリスト)x軸 plt.xticks(軸の目盛のリスト)y軸ラベル plt.ylabel('ラベル')x軸ラベル plt.xlabel('ラベル')補助線の追加 plt.minorticks_on()plt.grid(which='both')表示領域 plt.ylim(min,max)plt.xlim(min,max)plt.show()でグラフを出力.
ポップアップウィンドウでグラフが表示されます.
- グラフの保存
ポップアップウィンドウの保存ボタンを押すことで画像に名前をつけて保存することが可能です.

例えば,以下のコードで次のグラフが表示されます.
np.arange(0,100,1)は,0から100までの数値を1ずつ増えるnumpyの配列を生成しています.
[x for x in range(0,101,1)] でも同様の結果となります.
plt.plot(np.arange(0,100,1)
,np.arange(0,100,1)
,color='red'
,label='sample')
plt.title('title')
plt.ylim(0,100)
plt.xlim(0,100)
plt.xticks(np.arange(0,100,10))
plt.yticks(np.arange(0,100,10))
plt.minorticks_on()
plt.grid(which='both')
plt.xlabel('x_label')
plt.ylabel('y_label')
plt.legend()
plt.show()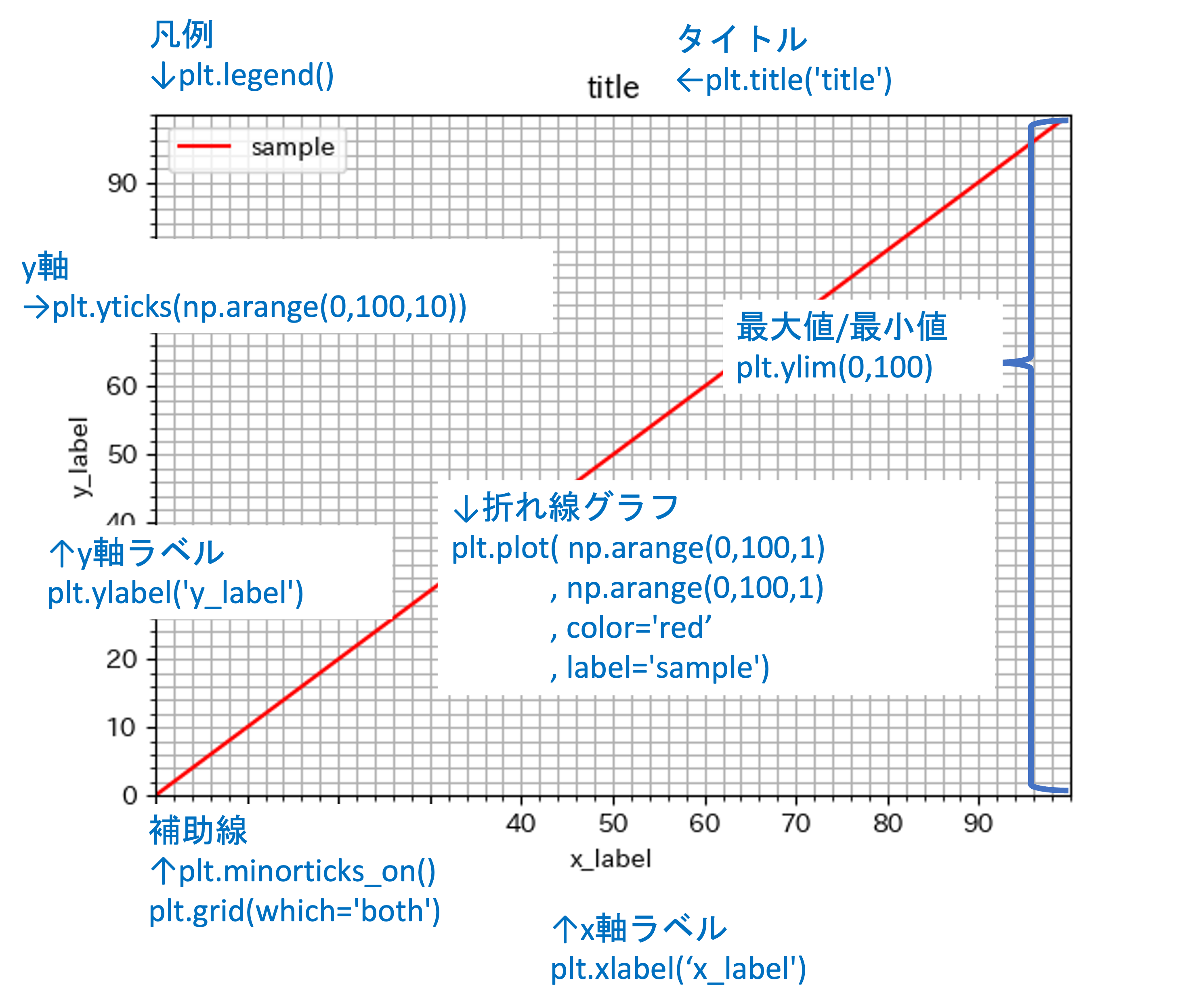
画像はplt.show()で表示されるポップアップウィンドウを立ち上げなくても,plt.savefig('figure.png')と記述することで保存することができます.
ただし,plt.show()をして自分でポップアップウィンドウを閉じないと,plt.による設定がメモリに保存されたままになります.
plt.show()を実行しない場合は必ず最後にplt.close()を追加してメモリを開放しましょう.
plt.plot(np.arange(0,100,1)
,np.arange(0,100,1)
,color='red'
,label='sample')
plt.savefig('figure.png')
plt.close()1.1.1 棒グラフの作成
こちらからデータをダウンロードし,棒グラフを作成してみましょう.
まずはデータを確認します.
# import 部分は省略されています
# dataフォルダにあるbar_pie.csvというファイルを読み込みます.
df = pd.read_csv("data/bar_pie.csv")
# 読み込んだファイルの中身を見てみます.
print(df)
"""
cat dog bird
0 10 12 20
"""プログラムは読み込むデータと,作りたいグラフの形によって変化します. どのようなデータが必要かを意識して,データを抽出しましょう.
棒グラフの作成に必要なデータは,
棒毎のラベル
それぞれの棒の名前です.文字列で指定します.
今回は'cat','dog','bird'とします.
棒毎のx軸の位置
棒グラフの位置は,0から始まる整数の列として指定します.
今回は,0,1,2を指定します.
棒毎の高さになります.
高さに10,12,20を指定します.
# 棒グラフのラベルを抽出します
# df.columns でDataFrameからHeaderを抽出し,
# list()関数でDataFrameからlist型に変換しています
labels = list(df.columns)
# 棒グラフのx軸のどこに置くのかを指定しています.
# np.arange(x) は [0,1,..,x]というarrayを作ります.
x_position = np.arange(len(labels))
#棒グラフの高さを抽出します
# メソッド icloc[x]はDataFrameのx行目を抽出します.
values = list(df.iloc[0])抽出した情報を元に,棒グラフを作成します.
plt.bar(X軸のリスト,Y軸のリスト)の形で,データを指定します.
# 棒グラフを作成します.
# x 軸 にx_position
# それぞれの棒グラフの高さにvaluesを与えています.
# その他にも沢山の引数があります.
plt.bar(x=x_position, height=values)このままだと,X軸のラベルに何も記述されないので,
plt.xticks(ラベルの位置のリスト,ラベルのリスト)で,ラベルを指定します.
#ラベルの位置を指定します.
plt.xticks(ticks=x_position,labels=labels)
# Y軸ラベルを指定します
plt.ylabel("number")
# タイトルを指名します
plt.title("kind")
# グラフの表示
plt.show()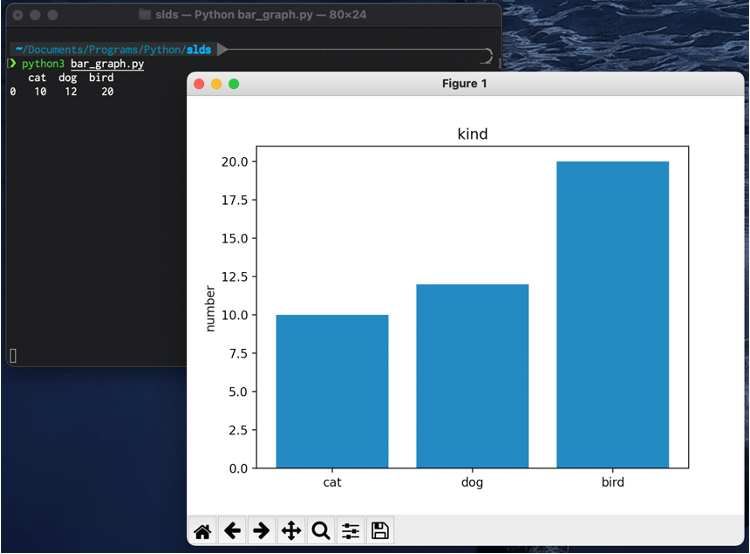
表示されたグラフは, 保存ボタンで画像として保存できます.
グラフ作成の基本は,これで終わりです.あとは,それぞれのグラフ毎にplt.bar()の部分を使い分け,グラフのデザインを変更することで,様々なグラフが作成できます.
グラフのデザインに関する要素は,無数にあるためこの講義ですべてを扱うことはできませんが,いくつかの要素を実際に変更してみましょう.
1.1.2 色の変更
matplotlibではグラフの各部に以下の色を指定できます. これ以外の指定の仕方もあります.色の変え方は,それぞれのグラフで異なります.

棒グラフはplt.bar(color=棒毎の色のリスト)の形で棒ごとに色を指定することができます.
# 棒グラフの色を指定します.
# 1つ目 red
# 2つ目 blue
# 3つ目 yellow
color_list = ["red", "blue", "yellow"]
# 引数に色の指定をします
plt.bar(color=color_list, x=x_position, height=values)
#ラベルの位置を指定します.
plt.xticks(ticks=x_position,labels=labels)
# yラベルを指定します
plt.ylabel("number")
# タイトルを指名します
plt.title("kind")
# グラフの表示
plt.show()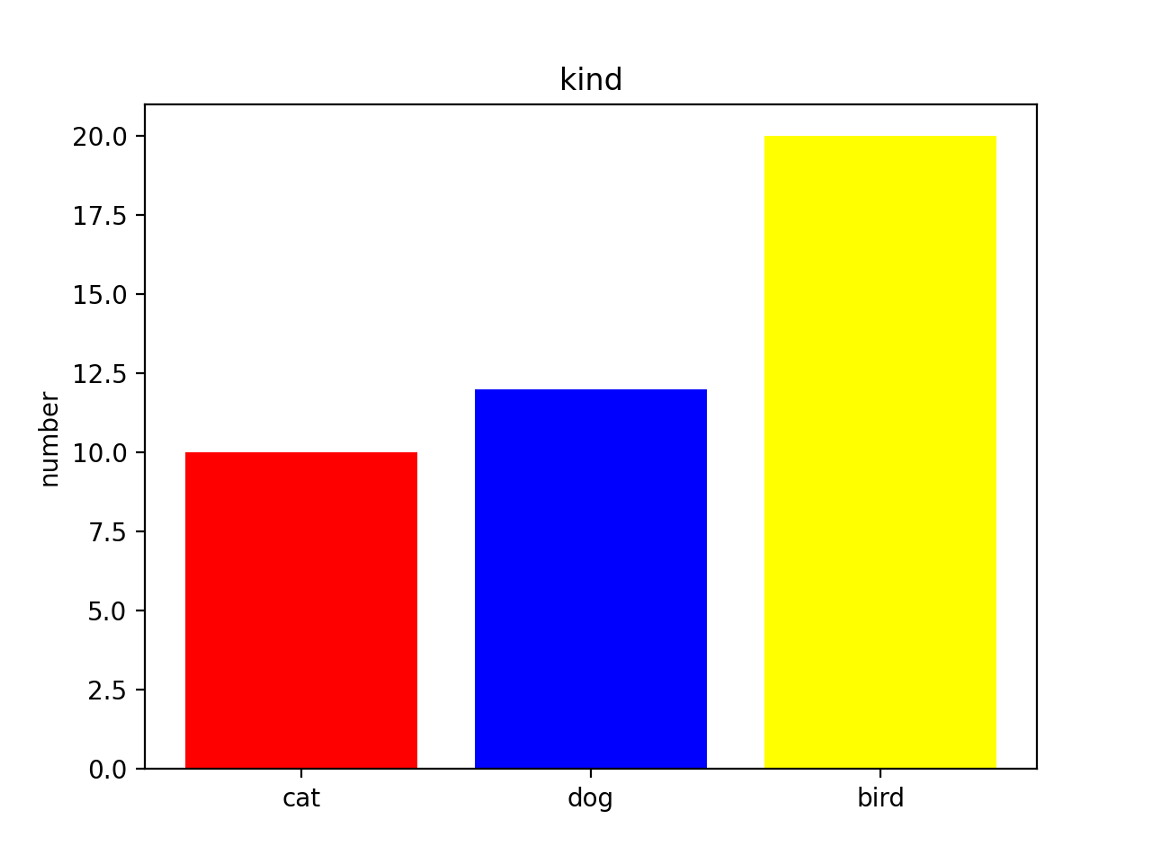
1.1.3 スタイルの変更
毎回細かなデザインを自分で調整すると手間なので,デフォルトで準備されているスタイルを利用すると楽です.
matplotlibではいくつかのデフォルトのスタイルが準備されています. 使用可能なスタイルは,plt.style.available で確認できます.
❯ python
Python 3.12.3 (main, Jun 3 2024, 08:31:31) [Clang 15.0.0 (clang-1500.3.9.4)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import matplotlib.pyplot as plt
>>> plt.style.available
['Solarize_Light2', '_classic_test_patch', '_mpl-gallery', '_mpl-gallery-nogrid', 'bmh', 'classic', 'dark_background', 'fast', 'fivethirtyeight', 'ggplot', 'grayscale', 'seaborn-v0_8', 'seaborn-v0_8-bright', 'seaborn-v0_8-colorblind', 'seaborn-v0_8-dark', 'seaborn-v0_8-dark-palette', 'seaborn-v0_8-darkgrid', 'seaborn-v0_8-deep', 'seaborn-v0_8-muted', 'seaborn-v0_8-notebook', 'seaborn-v0_8-paper', 'seaborn-v0_8-pastel', 'seaborn-v0_8-poster', 'seaborn-v0_8-talk', 'seaborn-v0_8-ticks', 'seaborn-v0_8-white', 'seaborn-v0_8-whitegrid', 'tableau-colorblind10']それぞれのスタイルのイメージはこちらで確認できます.
スタイルはplt.style.use('スタイル名')で指定し,以降のコード全てに適用されます.
# スタイル 'ggplot' を使ってみます
plt.style.use('ggplot')
# 引数に色の指定をします
plt.bar(x=x_position, height=values)
#ラベルの位置を指定します.
plt.xticks(ticks=x_position,labels=labels)
# yラベルを指定します
plt.ylabel("number")
# タイトルを指名します
plt.title("kind")
# グラフの表示
plt.show()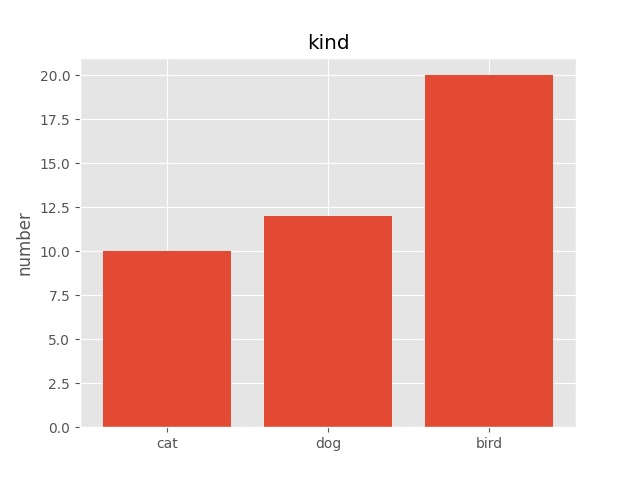
1.1.4 要素の追加
グラフに新しい要素を付け加えるのも簡単です.
plt.show()までの間に,グラフを宣言することで,複数のグラフを重ねることが可能です.
ここでは, 異なる色の棒グラフを追加しています.
また, plt.legend()によって凡例を追加しています.
# スタイル seaborn を使ってみます
plt.style.use('seaborn')
# 棒グラフを2つ並べます
plt.bar(color='red', x=x_position, width=0.3,height=values)
plt.bar(color='blue',x=x_position+0.3, width=0.3,height=[11,15,14])
#凡例を追加します
# loc で位置を指定します
# 上下 upper center lower
# 左右 left center right
plt.legend(['2020','2000'], loc='upper left')
#ラベルの位置を指定します.
plt.xticks(ticks=x_position+0.15,labels=labels)
# yラベルを指定します
plt.ylabel("number")
# タイトルを指名します
plt.title("kind")
# グラフの表示
plt.show()
デザインのすべてのパターンをここで扱うことは出来ないので, やりたいことに応じて, matplotlubの公式ドキュメントを確認しましょう.
1.2 円グラフ
先ほどと同じデータbar_pie.csvを利用して円グラフを作成してみます.
"""
header1 header2 header3 ...
value1 value2 value3 ...
の形のcsvから棒グラフを作成する
"""
# dataフォルダにあるbar_pie.csvというファイルを読み込みます.
df = pd.read_csv("data/bar_pie.csv")
# 読み込んだファイルの中身を見てみます.
print(df)
# 棒グラフのラベルを抽出します
# df.columns でDataFrameからHeaderを抽出し,
# list()関数でDataFrameからlist型に変換しています
labels = list(df.columns)
# メソッド icloc[x]はDataFrameのx行目を抽出します.
values = list(df.iloc[0])
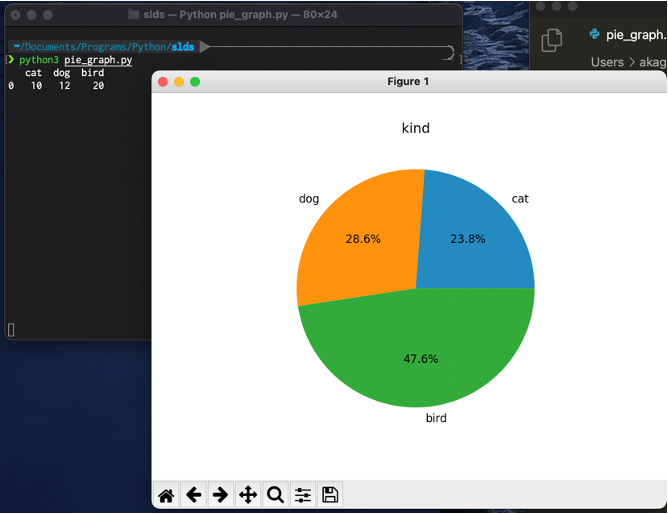
# 円グラフの作成
plt.pie(values, labels=labels, autopct='%1.1f%%')
# タイトルを指名します
plt.title("kind")
# グラフの表示
plt.show()円グラフは, plt.pie()にそれぞれの領域の割合と,ラベルを与えることで,作成できます.
グラフに数字を表示するには,autopct=にフォーマット文字列で表示内容を指定します.
上記の例では'%1.1f%%'と書くことで,小数点1桁まで数値を表示しています.
- 演習
円グラフデータ,折れ線グラフデータ2,棒グラフデータ3を利用し,それぞれのグラフを作成してください. 表示が必要だと思われるデザインを設定してください.
1.3 for文を利用したグラフ
これまでのように単純な一つのグラフを作成するだけであれば,恐らくExcelなどのほうが手軽ですが,多数のグラフを作成したり, 複数のデータを組み合わせた複雑なグラフを作成する場合にはプログラミングの方が便利になります.
例えばこちらのデータを利用して棒グラフを作成することを考えてみましょう.このデータは10箇所の気温が記録された時系列データです.
Date Location_1 Location_2 ... Location_8 Location_9 Location_10
0 2023-01-01 18.211700 21.553371 ... 18.665620 29.108637 21.634069
1 2023-01-02 15.108630 16.172744 ... 20.135756 9.212193 24.209877
2 2023-01-03 14.938279 24.593193 ... 16.778431 22.291269 19.815977
3 2023-01-04 20.640249 18.862405 ... 13.282269 16.040627 15.993132
4 2023-01-05 14.218562 16.281882 ... 15.729466 24.951213 18.053277
.. ... ... ... ... ... ... ...
95 2023-04-06 21.312739 19.613363 ... 16.497553 20.446656 13.644605
96 2023-04-07 26.388210 31.533854 ... 18.999736 15.603714 19.215097
97 2023-04-08 16.914329 20.479892 ... 21.698464 17.705697 16.867517
98 2023-04-09 14.316258 17.841650 ... 31.885071 20.816917 16.895196
99 2023-04-10 23.595042 19.896247 ... 17.534881 15.180066 15.104460このデータのLocation_1からLocation_10までの折れ線グラフを一つのグラフに表示することを考えてみます.
matplotlibでは, plt.show()までに要素を重ねることで複数のグラフを重ねることができます.
例えば,10本の折れ線グラフを表示する場合,一つ一つ手書きすると以下のようになります.
df = pd.read_csv('data/temperature_10location.csv')
print(df)
#'Date'列を日付型に変更しています.
df['Date'] = pd.to_datetime(df['Date'])
#一つ一つ手書きする方法
plt.plot(df['Date'],df['Location_1'],label='Location_1')
plt.plot(df['Date'],df['Location_2'],label='Location_2')
plt.plot(df['Date'],df['Location_3'],label='Location_3')
plt.plot(df['Date'],df['Location_4'],label='Location_4')
plt.plot(df['Date'],df['Location_5'],label='Location_5')
plt.plot(df['Date'],df['Location_6'],label='Location_6')
plt.plot(df['Date'],df['Location_7'],label='Location_7')
plt.plot(df['Date'],df['Location_8'],label='Location_8')
plt.plot(df['Date'],df['Location_9'],label='Location_9')
plt.plot(df['Date'],df['Location_10'],label='Location_10')
plt.legend()
plt.xticks(rotation=15) #x軸を15度傾かせています
plt.show()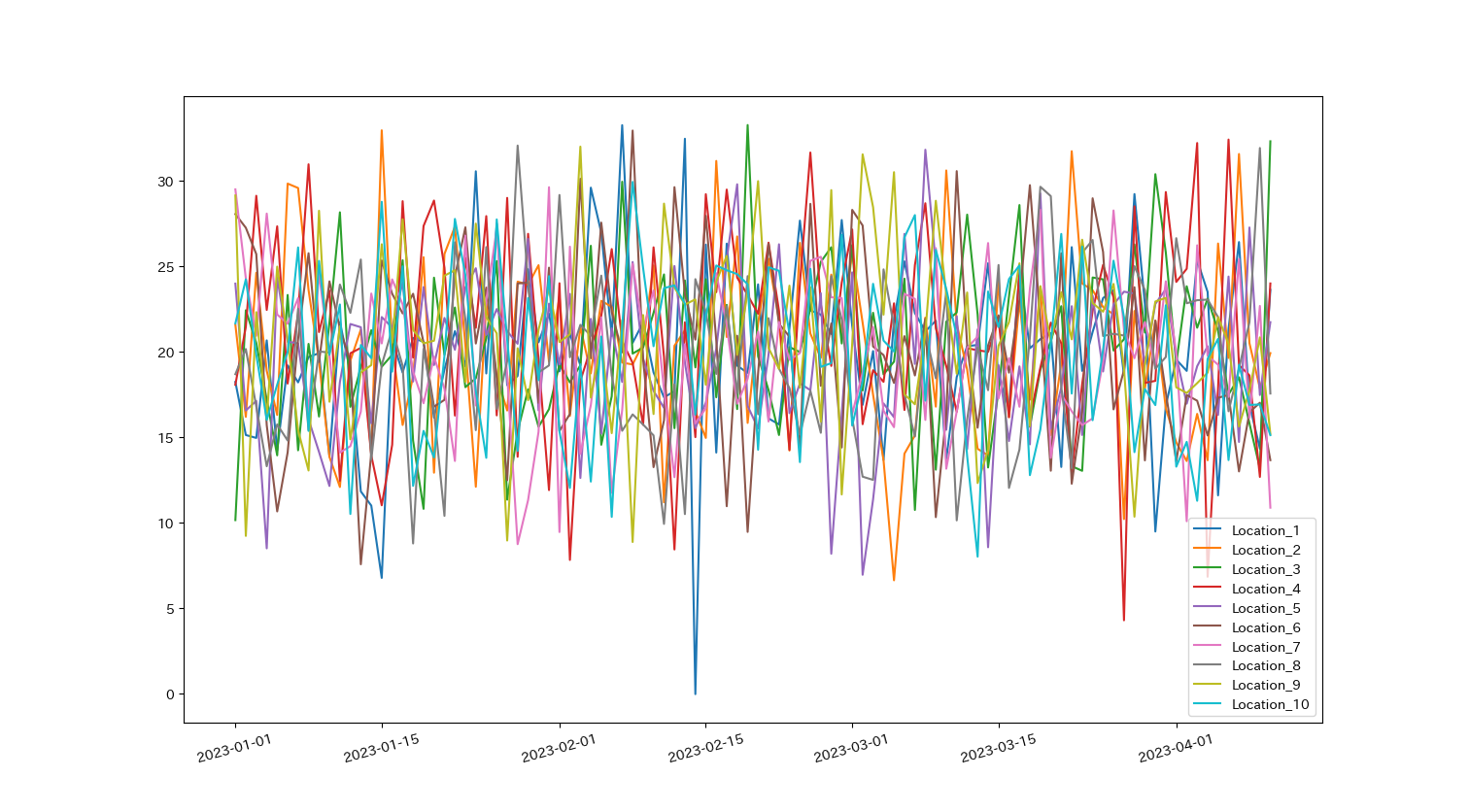
10本程度であれば,まだ書けなくもありませんが,それでも手間がかかります.こういった繰り返しの作業はfor文を利用しましょう.
for文を利用した場合には以下のようになります.
for x in df.columns[1:]:
plt.plot(df['Date'],df[x],label=x)
plt.legend()
plt.xticks(rotation=15)
plt.show()グラフの内容は同じですが,こちらのほうが労力が少なく,コードもスッキリしており,何か修正を加える場合でも修正箇所が少なくて済みます.
繰り返し作業は積極的にfor文やwhile文を利用するようにしましょう.
1.4 グラフの分割
先程は一つのグラフ内に複数の折れ線グラフを表示しましたが,個別に表示する場合にはどのようになるでしょうか.
一つの方法として,以下の用に複数のグラフを個別に作成することも可能です.
(先に保存先のディレクトリ result/multi_plot を作成しておきましょう.)
for x in df.columns[1:]:
plt.plot(df['Date'],df[x])
plt.title(x)
plt.xticks(rotation=15)
plt.savefig('result/multi_plot/' + x + '.png')
plt.close()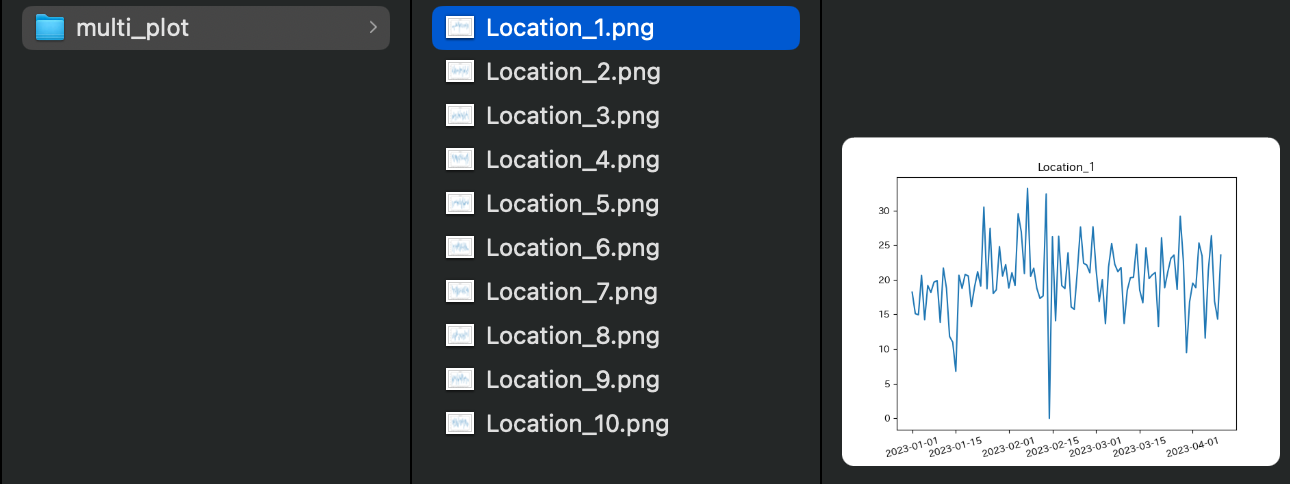
しかし,レポートなどに10枚の画像を貼り付けるのは手間がかかりますし,余白など無駄も多いです.
- subplots()
matplotlibには1枚の画像を分割して複数のグラフを載せるためのメソッド.subplots()があるので,関連するグラフや比較のためのグラフなどはできるだけ1枚の画像に集約しましょう.
.subplots()は1枚の画像をn行,n列に分割し,それぞれの領域にグラフを描画します.
各領域は axesなどと呼ばれ,画像全体をfigureなどと呼びます.
利用するためには,まず fig, axes = plt.subplot()の形で宣言します. 引数として,行数はnrows=,列数はncols=にそれぞれintで指定します.
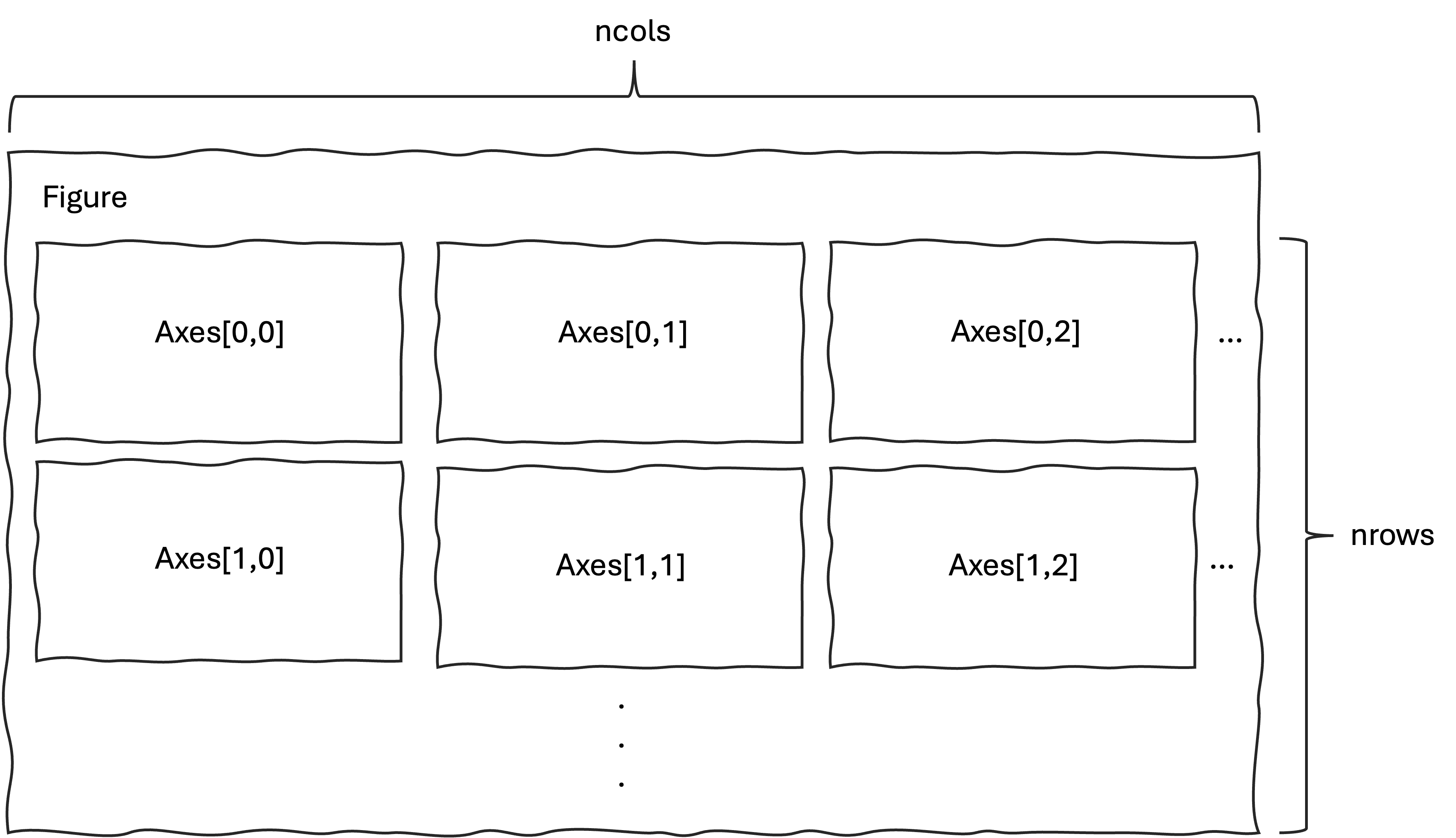
fig, axes = plt.subplot(nrows= 5 #行数の指定
,ncols= 2 #列数の指定
)宣言のあと,各領域のグラフを axes[行,列]の形で指定していきます.行や列は0から始まるので注意してください.
axes[0,0].plot(df['Date'],df['Location_1'],label='Location_1')
axes[0,1].plot(df['Date'],df['Location_2'],label='Location_2')
axes[1,0].plot(df['Date'],df['Location_3'],label='Location_3')
axes[1,1].plot(df['Date'],df['Location_4'],label='Location_4')
axes[2,0].plot(df['Date'],df['Location_5'],label='Location_5')
axes[2,1].plot(df['Date'],df['Location_6'],label='Location_6')
axes[3,0].plot(df['Date'],df['Location_7'],label='Location_7')
axes[3,1].plot(df['Date'],df['Location_8'],label='Location_8')
axes[4,0].plot(df['Date'],df['Location_9'],label='Location_9')
axes[4,1].plot(df['Date'],df['Location_10'],label='Location_10')
plt.show()以下のようなグラフが作成されます. しかし, 少し見にくいですね.
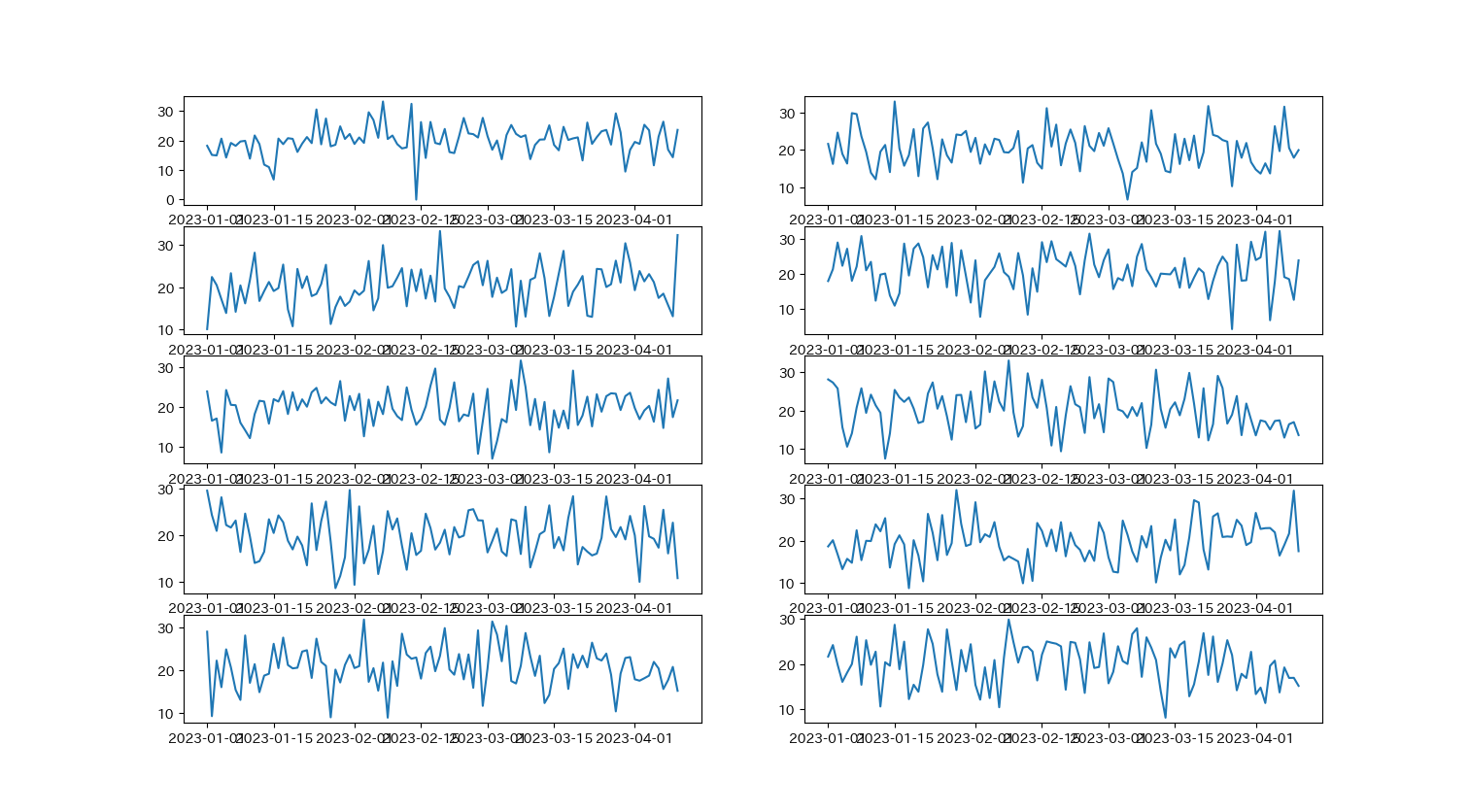
.subplots(sharex=True)とすると,x軸を共有することができます.今回のグラフはx軸がすべて同じなので,共有してみましょう.
また,それぞれのグラフにタイトルを付けてみます.
更に,一つ一つ手で入力するのは手間なのでfor文を利用してみましょう.
タイトルを付けるには今までのplt.title()ではなくaxes[r,c].set_title()になります. axes毎の要素に関しては公式サイトを参考にしてください.
fig, axes = plt.subplots(nrows= 5 #行数の指定
,ncols= 2 #列数の指定
,sharex=True)
count = 0
for i in range(5):
for j in range(2):
col = df.columns[1:]
axes[i,j].plot(df['Date'],df[col[count]])
axes[i,j].set_title(col[count])
axes[i,j].tick_params(axis='x', rotation=15)
count +=1
plt.show()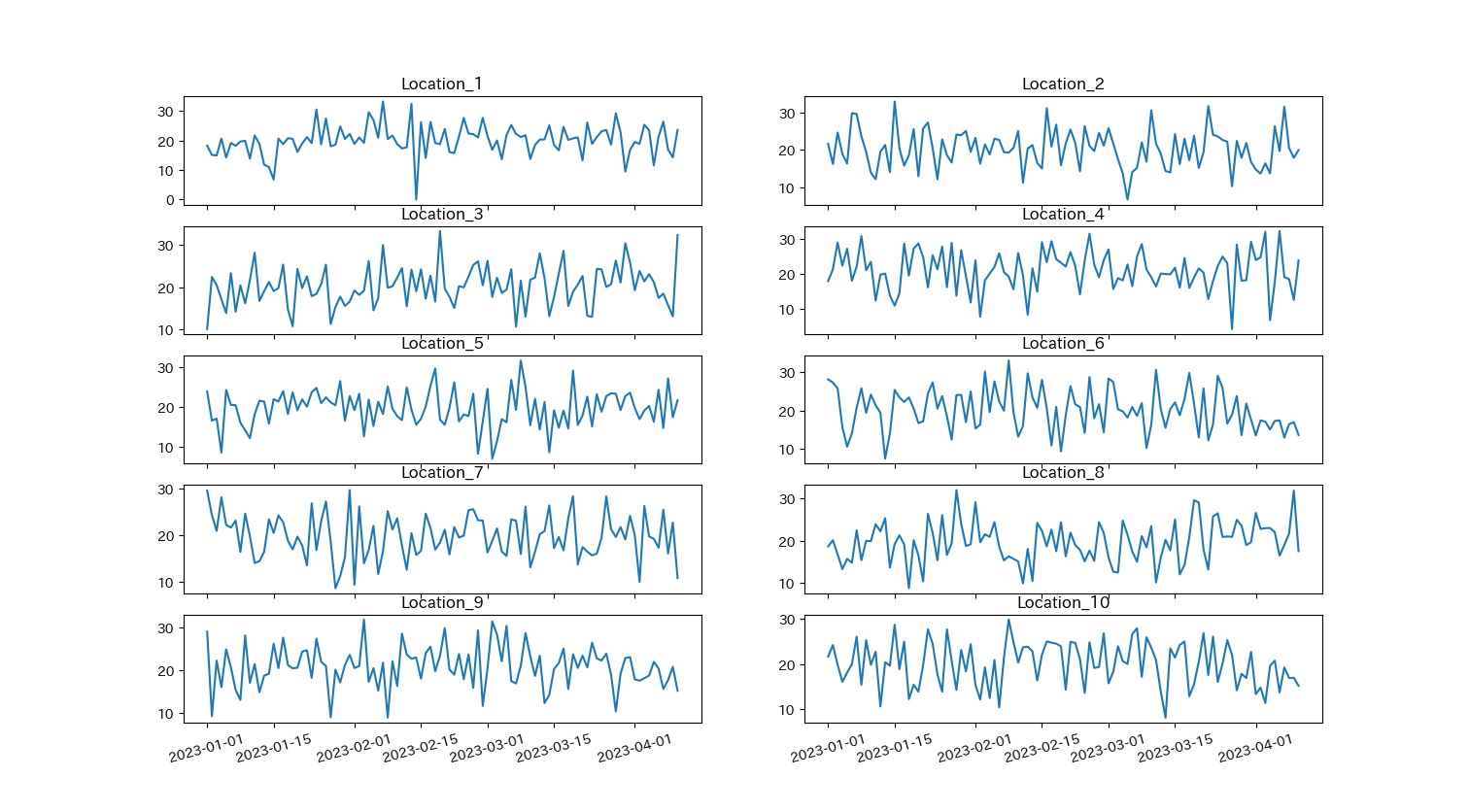
グラフ全体の要素はfig.の形で指定します.
タイトルを付ける場合はfig.suptitle('title')となります.
fig, axes = plt.subplots(nrows= 5 #行数の指定
,ncols= 2 #列数の指定
,sharex=True)
count = 0
for i in range(5):
for j in range(2):
col = df.columns[1:]
axes[i,j].plot(df['Date'],df[col[count]])
axes[i,j].set_title(col[count])
axes[i,j].tick_params(axis='x', rotation=15)
count +=1
fig.suptitle('subplots title')
plt.show()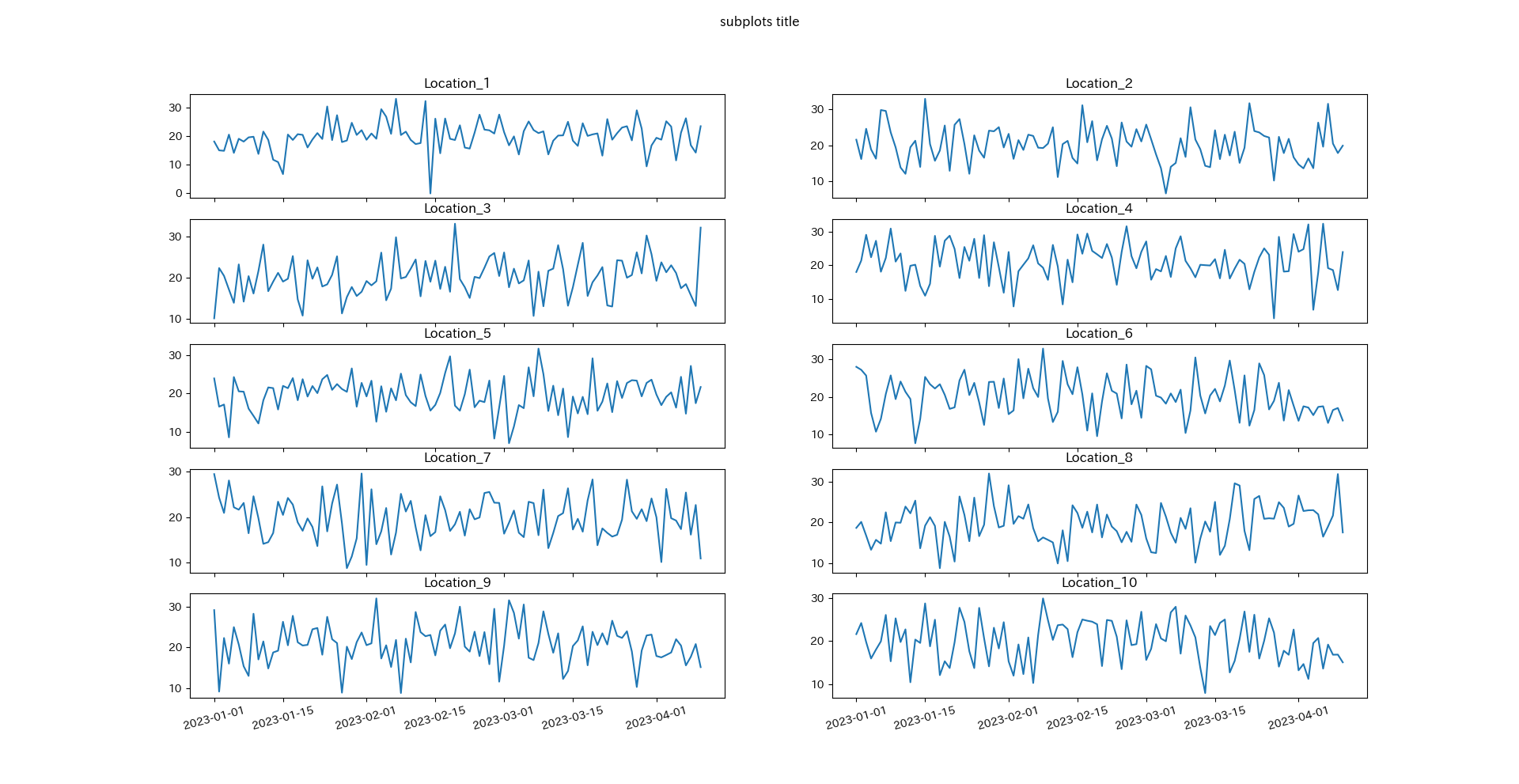
- flatten()
for文を二重ループで記述するのは大変なので,しばしばaxes.flatten()を利用して,連番に変換すると便利です.
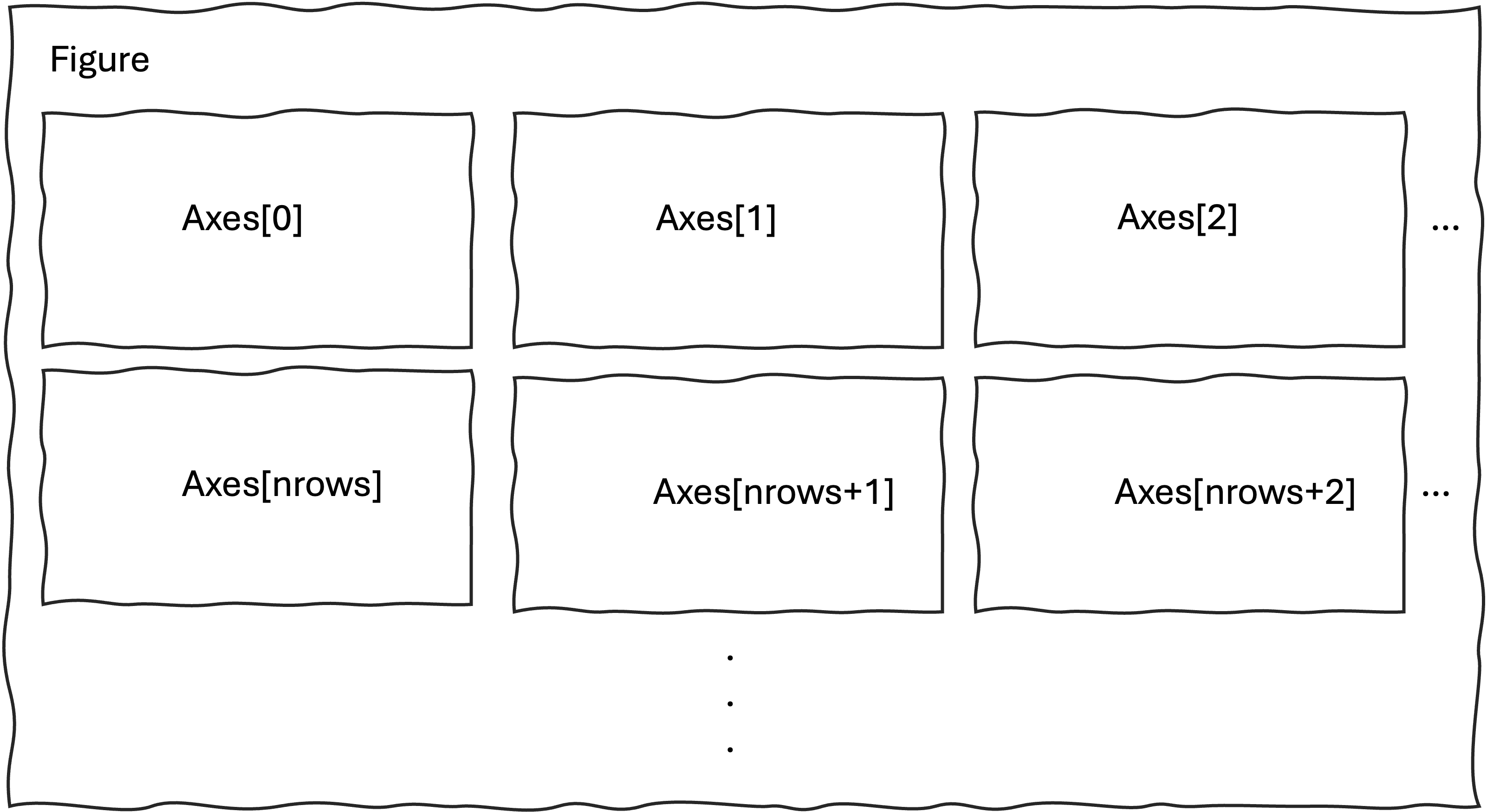
fig, axes = plt.subplots(nrows= 5 #行数の指定
,ncols= 2 #列数の指定
,sharex=True)
#連番に変換
axes = axes.flatten()
for i in range(10):
col = df.columns[1:][i] #countをiで共通化
axes[i].plot(df['Date'],df[col])
axes[i].set_title(col)
axes[i].tick_params(axis='x', rotation=15)
fig.suptitle('subplots title')
plt.show()1.5 度数分布表とヒストグラム
データを手に入れたら最初にデータを可視化してデータの特徴を掴む必要があります. データの特徴として重要なものに,データの分布があります.
分布の意味
分布という語の詳細な意味に関しては,後ほど検定や回帰の章でも簡単に扱いますが,統計学入門において数理的に詳しく扱っています.
統計学入門を履修していない人はここでは,単にデータの散らばり具合という意味として捉えておきましょう.
分布を可視化する手法として代表的なものに,度数分布表と,ヒストグラムがあります. 1次元のデータの可視化において,度数分布表とヒストグラムは,データ分析のファーストステップとも称される,重要な手法です. データを手に入れたらまずは度数分布表と,ヒストグラムを作成してみましょう.
1.5.1 度数分布表
度数分布表とは,データの数を区切られた範囲ごとに数え上げた表のことです. 質的データの場合は,データのカテゴリー毎に,量的データの場合は分析者が定めた区間毎にデータがいくつかるのかを数え上げます.
普通ヒストグラムというと,量的データを対象としたものをいいますが,ここではわかりやすさのために,質的データから見ていきましょう.
以下の表は,何かしらの商品の美味しさに関するアンケート結果です. 商品を食べて,「とても美味しい」と回答した人の人数が9人,「不味い」と回答した人の人数が5人であることなどがわかります.
このようにデータのカテゴリー別にその値が生じたケースの数を度数といい,度数を数え上げ表に整理したものを度数分布表といいます.
| アンケート区分 | 度数 |
|---|---|
| とても美味しい | 9 |
| どちらかといえば美味しい | 11 |
| 普通 | 34 |
| どちらかといえば不味い | 5 |
| 不味い | 5 |
度数の亜種には,以下のようなものがあり,それぞれによってデータの分布が把握できます.
累積度数:
順序尺度データの度数を少ない方から足し上げた値
相対度数(構成比率):
度数の総和を100%としたときの構成比率
累積相対度数(累積比率):
相対度数を上から足し上げた値
| アンケート区分 | 度数 | 累積度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| とても美味しい | 9 | 9 | 14% | 14% |
| どちらかといえば美味しい | 11 | 20 | 17% | 31% |
| 普通 | 34 | 54 | 53% | 84% |
| どちらかといえば不味い | 5 | 59 | 8% | 92% |
| 不味い | 5 | 64 | 8% | 100% |
| 計 | 64 | 100% |
度数分布表を作成することで,データがどの分類に偏っているのかなど,データの分布の傾向がつかめます. 度数分布表を見る場合には,相対度数や累積度数からデータが一番多いカテゴリー,度数データの過半数が属するカテゴリー,データのほとんど(90%程度)が属するカテゴリーなどに注目してみましょう. 上のデータでは,最も回答が多いのは「普通」であること, 「とても美味しい」「どちらかといえば美味しい」の回答が,31%であるのに対して,「どちらかといえば不味い」「不味い」の回答が18%であり,全体的にこの商品の味は高評価側に集中していることなどがわかります.
Pythonで度数分布表を作成するにはどのようにしたら良いのでしょうか. 質的データの場合は,ただそれぞれの値を数えればいいので,for文などを利用することも可能ですが,pandasのvalue_counts()メソッドを利用することで簡単に作成できます.
こちらのとある授業の難易度に関する質的データをダウンロードして度数分布表を作成してみましょう.
データは以下のように,「難しすぎてついていけない」,「難しいが許容できる」,「ちょうどよい」,「簡単だが許容できる」「簡単すぎて退屈」の5段階のカテゴリーが記述されています.
Diff
0 難しいが許容できる
1 簡単すぎて退屈
2 難しいが許容できる
3 簡単だが許容できる
4 ちょうどよい
.. ...import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import japanize_matplotlib
import math
import module.sturges as st
#データの読み込み
df = pd.read_csv('Data/diff.csv')
print(df)
#ヒストグラムを作りたいデータの列名を指定
target_column = 'Diff'
#度数
freq = df[target_column].value_counts(sort=False)
#順番の入れ替え
freq = freq.reindex(['難しすぎてついていけない'
,'難しいが許容できる'
,'ちょうどよい'
,'簡単だが許容できる'
,'簡単すぎて退屈'],axis='index')
print('度数',freq)
rel_freq = freq / df[target_column].count() # 相対度数
cum_freq = freq.cumsum() # 累積度数
rel_cum_freq = rel_freq.cumsum() # 相対累積度数
dist = pd.DataFrame(
{ "Value": freq.index, #階級値
"Freq": freq, #度数
"Rel": rel_freq, #相対度数
"Cum": cum_freq, #累積度数
"RelCum": rel_cum_freq, #相対累積度数
},
index=freq.index
)
print(dist)
dist.to_csv('frequency_table.csv',)保存されたcsv(frequency_table.csv)を確認してみると,度数分布表が作成されていることが確認できます.
| Value | Freq | Rel | Cum | RelCum |
|---|---|---|---|---|
| 難しすぎてついていけない | 2 | 0.02247191 | 2 | 0.02247191 |
| 難しいが許容できる | 44 | 0.494382022 | 46 | 0.516853933 |
| ちょうどよい | 38 | 0.426966292 | 84 | 0.943820225 |
| 簡単だが許容できる | 4 | 0.04494382 | 88 | 0.988764045 |
| 簡単すぎて退屈 | 1 | 0.011235955 | 89 | 1 |
質的データはあらかじめデータのカテゴリーが定められているのでその数を数えるだけで,度数分布表が作成できました. それでは,カテゴリーが存在しない量的データではどのようにして度数分布表を作成するのでしょうか.
- 量的データと度数分布表
量的データには当てはまるデータを数えるためのカテゴリーが存在しません. 年収のデータを考えた場合,年収1万円ごとに表を作ると1から数億まで,非常に細かくなります. そこで,量的データで度数分布表を作成するには,100万円ごと,300万円ごとなどデータをいくつかの区間に分けて,区間別の度数を数える必要があります. ここで, 作られた区間を階級,階級の幅を階級幅,階級を代表する値を階級値といいます. 階級値は大抵の場合,区間の中間の値が用いられます(100万円~200万円の区間だとすると,150万円など).
以下の度数分布表は,ある情報クラスの成績(0-100点)を10点毎に区分したものです. それぞれの点数に当てはまる人数を数えて度数とします.
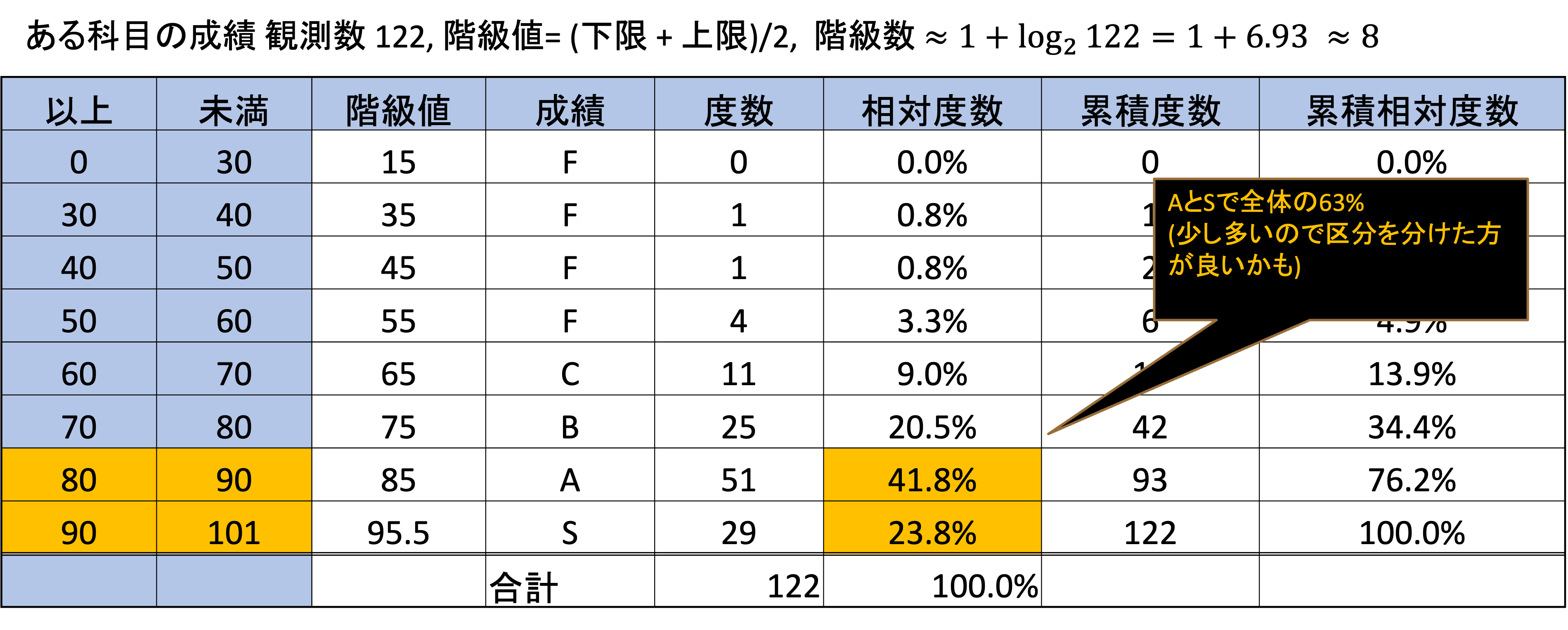
量的データの階級数や階級幅は,100万円ごとなどある程度人間の判断によって作成しても構いませんが,数理的に決定する方法もあります.
階級幅は階級数が決まることで自動的に決まるため,階級数を決める一般的な目安として,スタージェスの公式が利用されます.
観測数をn,階級数をkとすると.
k = 1 + log_2 n = \frac{log_{10} n}{log_{10} 2}
程度のkが望ましいとされています.
計算結果はおおよそ以下のようになります.

Pythonではスタージェス数は対数計算をするためのモジュールmathを利用して以下のように求めることができます.
# 2進対数を返す math.log2() 関数などを利用するために必要なモジュール
import math
# 関数名を sturgesNumber として引数をnとします
def sturgesNumber(n):
# 公式の通り k = 1 + log2 n
# 階級数は整数が良いので,math.floor()で小数点以下を切り捨てます
return (math.floor (1 + math.log2(n)))
print(sturges(2048)) #>>> 12階級数が決まることで階級幅が \frac{(データの最大値 - データの最小値)}{階級数}
として決まります.
それでは,こちらのデータを利用して,度数分布表を作成してみます. 量的データの度数分布表を作成するには,value-counts()の引数bins=に各階級の終点を表すリストを指定します.
#ヒストグラムを作りたいデータの列名を指定
target_column = 'Values'
# 関数名を sturgesNumber として引数をnとします
def sturgesNumber(n):
# 公式の通り k = 1 + log2 n
# 階級数は整数が良いので,math.floor()で小数点以下を切り捨てます
return (math.floor (1 + math.log2(n)))
# dataフォルダにあるhistogram_quantitative.csvというファイルを読み込みます.
df = pd.read_csv("data/histogram_quantitative.csv")
# 読み込んだファイルの中身を見てみます.
print(df)
#階級数を決定
stnum = sturgesNumber(len(df[target_column]))
print('sturges number:',stnum)
#階級幅を決定
space = int((df[target_column].max() - df[target_column].min()) / stnum)
print('space:',space)
#階級幅の終端を指定
bins = np.arange(start = int(df[target_column].min()) - 1 #最小値
,stop = int(df[target_column].max()) + 1 #最大値
,step = space #階級幅
)
print('bins:',bins)
#度数
freq = df[target_column].value_counts(bins =bins, sort=False)
print('度数',freq)
rel_freq = freq / df[target_column].count() # 相対度数
cum_freq = freq.cumsum() # 累積度数
rel_cum_freq = rel_freq.cumsum() # 相対累積度数
dist = pd.DataFrame(
{ "Value": freq.index, #階級値
"Freq": freq, #度数
"Rel": rel_freq, #相対度数
"Cum": cum_freq, #累積度数
"RelCum": rel_cum_freq, #相対累積度数
},
index=freq.index
)
print(dist)
dist.to_csv('frequency_table_qualitative.csv'
,encoding='utf-8-sig'
,index=False)結果作成された,frequency_table_qualitative.csvを開いてみると,以下のような度数分布表が作成されたことが確認できます.
| Value | Freq | Rel | Cum | RelCum |
|---|---|---|---|---|
| (8.999, 18.0] | 1 | 0.01 | 1 | 0.01 |
| (18.0, 27.0] | 5 | 0.05 | 6 | 0.06 |
| (27.0, 36.0] | 11 | 0.11 | 17 | 0.17 |
| (36.0, 45.0] | 21 | 0.21 | 38 | 0.38 |
| (45.0, 54.0] | 27 | 0.27 | 65 | 0.65 |
| (54.0, 63.0] | 20 | 0.2 | 85 | 0.85 |
| (63.0, 72.0] | 9 | 0.09 | 94 | 0.94 |
1.5.2 度数分布表の可視化:ヒストグラム
ここまでで,データの分布,偏りを把握する手段としての度数分布表を学びました. 度数分布表を眺めることである程度データの形は分かりますが,よりわかりやすく可視化する方法としてヒストグラムがあります.
ヒストグラム(Histogram)/柱状図とは,量的データの度数分布を棒グラフで表現したものです.ただし,通常の棒グラフと異なり値が連続しているので,棒と棒の間にスペースを置きません. 統計における最も基本的なグラフです.
ヒストグラムはいくつかの代表的なパターンがあり,それぞれ注意するべきポイントがありますので,順に見ていきましょう.
単峰型(unimodal)で左右対称
ヒストグラムの盛り上がっている部分を峰といいます. 峰の数が一つのヒストグラムを単峰(unimodal)なヒストグラムといいます.
ヒストグラムの基本となる形は,単峰で左右対称な分布です. この分布は,データが同質な集団から発生していることを表しています.
- 例:同じ人種の,同じ年代の,男性の集団の身長
- 例:同じ種類,同じ時期,同じ地域のうさぎの集団のサイズ峰からの左右のデータのばらつきは集団の個体差を表しています. 異なる,質を持つ集団が混じっている場合は峰が複数になることが多いです.

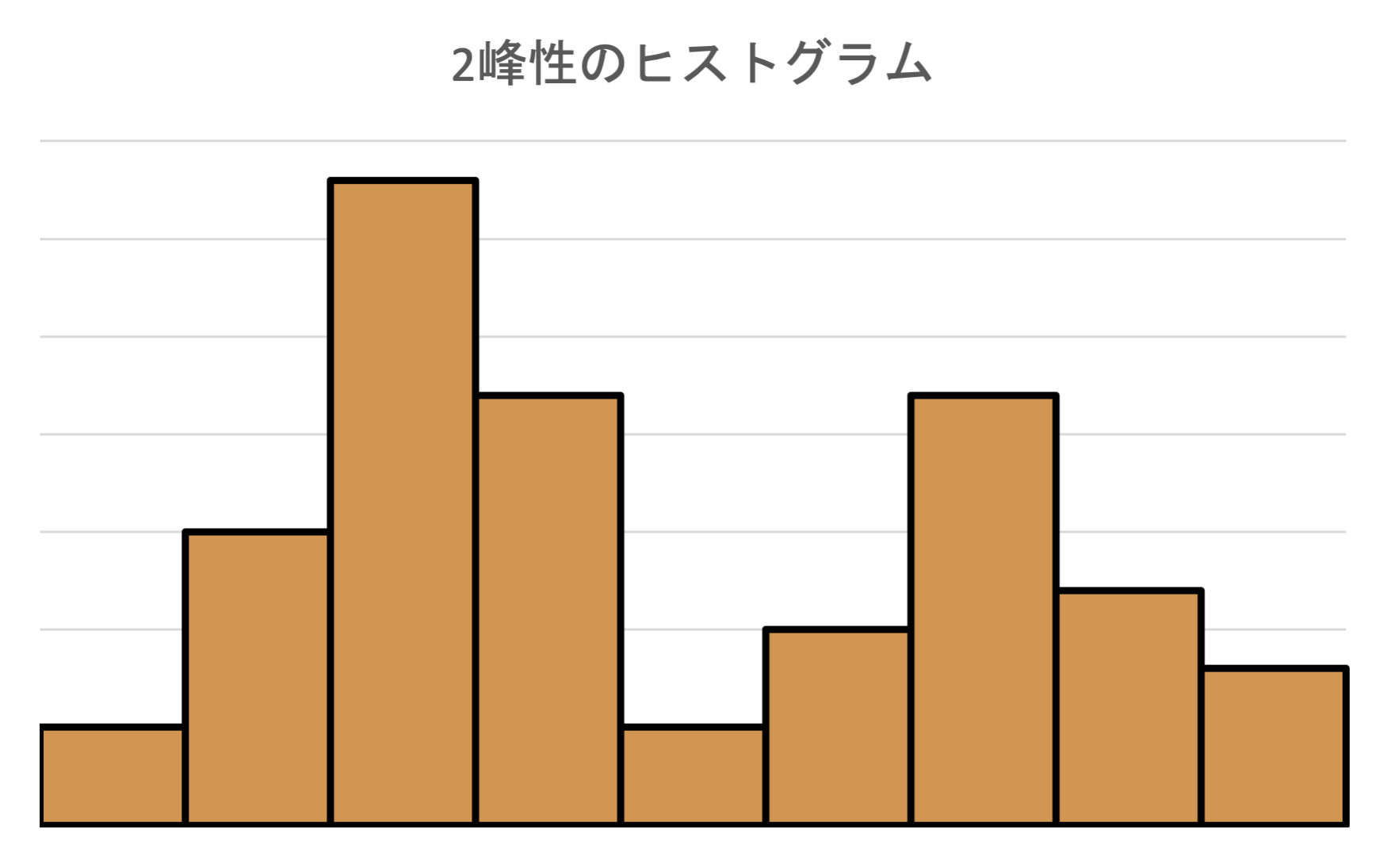
多峰型(bimodal)なヒストグラム
峰が2つ以上あるヒストグラムを多峰(bimodal)なヒストグラムといいます. 異質な集団が混ざっているデータでは,ヒストグラムが多峰になることがあります.
- 例:男女の混ざった集団の身長や体重
男性の峰と女性の峰が現れます.
- 例:小学生と中学生に同じテストを受けた点数
小学生の点数の峰と,中学生の点数の峰が現れます.ヒストグラムを作成し,多峰性が現れたらデータを集団別・要因別に分割して分析するのが良いとされています.データを特定の属性で分割することを層別といいます.
左右非対称なヒストグラム
ヒストグラムは峰を中心として左右対称な場合もありますが,どちらかの方向に歪んでいるものも良く見られます.
- 例:社会人の年収,企業の売上などヒストグラムの細くなっている部分をヒストグラムの尾といいます.
- **尾が**左に伸びている場合に **左に歪んだ分布**
- **尾が**右に伸びている場合に **右に歪んだ分布**といいます.
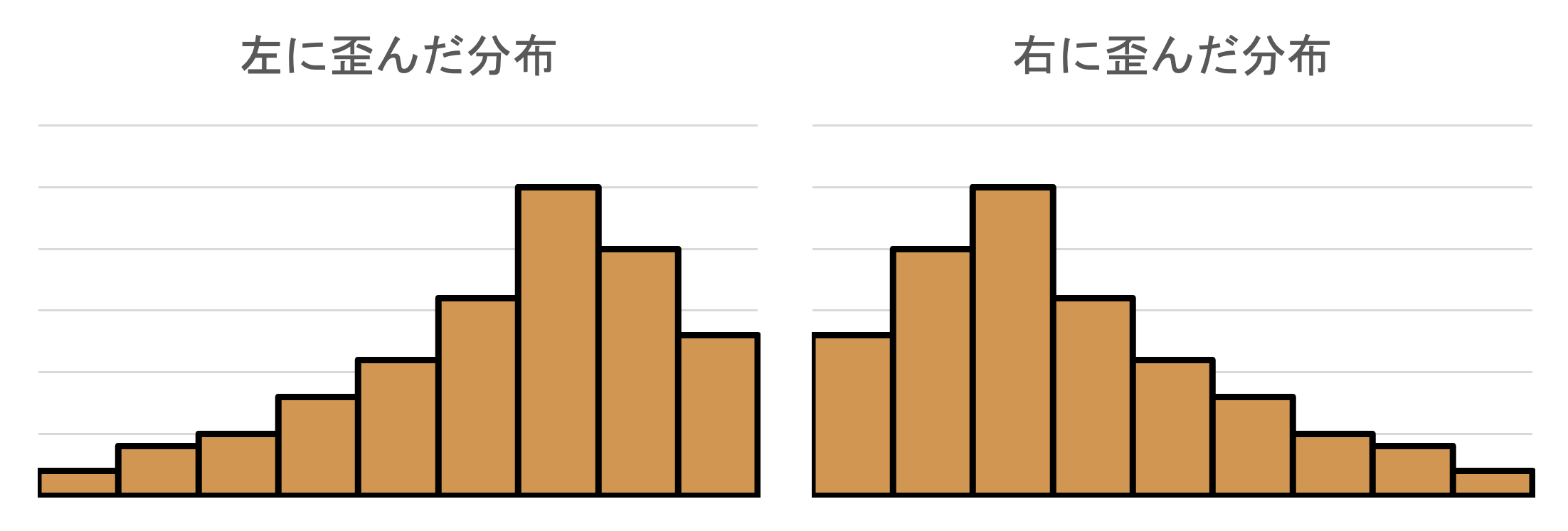
左右に歪んだ分布では,後に扱う中心を表す代表値(平均値や中央値)が適切に集団を代表しない場合があるので,代表値の使い分けが必要になります.
また, 後に扱う検定手法のうち,正規分布を仮定する検定が利用できないなど,手法の選択において,分布の歪みは重要なポイントです.
外れ値(Outlier)のあるヒストグラム
大多数のデータとは離れた位置にある少数のデータを外れ値(Outlier)といいます.
外れ値は,データ分析において非常に重要な意味を持ち,外れ値が現れた場合にはその原因を探ることが必要となります. 外れ値が発生する原因としては以下のようなものがあり,いずれも注目する必要があります.
- データの取得におけるミス
単純な入力ミスや計算ミスなど
発見した場合は修正,除外する必要がある.
- 異質な存在の発見
新種や新しい現象の発見などにつながる可能性があります.また,代表値の計算においては歪みが生じる可能性があるので,外れ値を除外する必要があります.
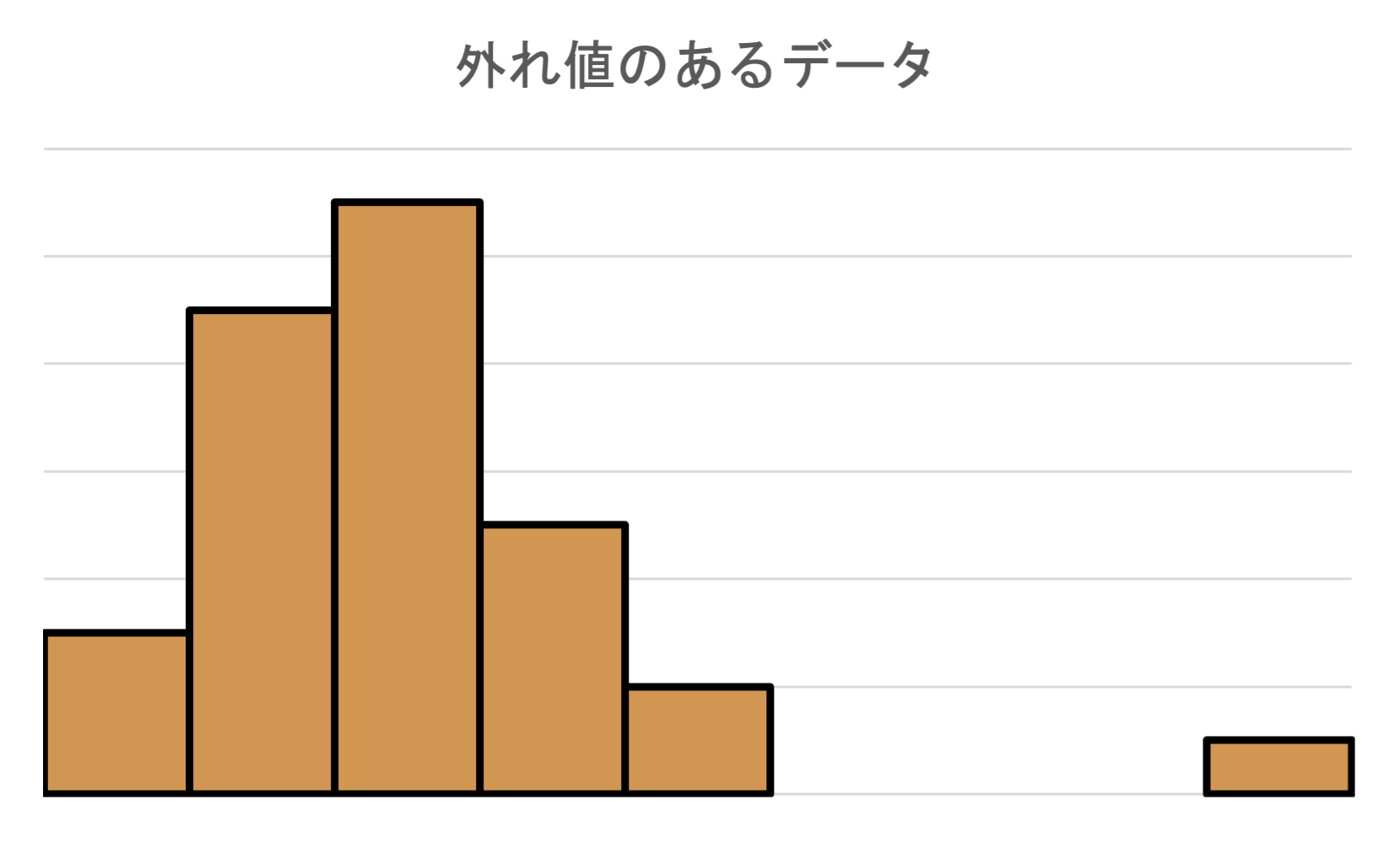
それでは,Pythonでヒストグラムを作成してみましょう. 度数分布表を作成している場合は,棒グラフを作成し,棒の幅を0にすることで,ヒストグラムが作成できます.
plt.bar()では,引数width=1を与えることで,棒の太さを1(棒の間を0)にすることができます.
まずは,以前扱った質的データの例におけるヒストグラムを作成してみましょう.
#データの読み込み
df = pd.read_csv('Data/diff_class.csv')
print(df)
#ヒストグラムを作りたいデータの列名を指定
target_column = 'Diff'
#度数
freq = df[target_column].value_counts(sort=False)
#順番の入れ替え
freq = freq.reindex(['難しすぎてついていけない'
,'難しいが許容できる'
,'ちょうどよい'
,'簡単だが許容できる'
,'簡単すぎて退屈'],axis='index')
print('度数',freq)
rel_freq = freq / df[target_column].count() # 相対度数
cum_freq = freq.cumsum() # 累積度数
rel_cum_freq = rel_freq.cumsum() # 相対累積度数
dist = pd.DataFrame(
{ "Value": freq.index, #階級値
"Freq": freq, #度数
"Rel": rel_freq, #相対度数
"Cum": cum_freq, #累積度数
"RelCum": rel_cum_freq, #相対累積度数
},
index=freq.index
)
print(dist)
dist.to_csv('frequency_table.csv',encoding='utf-8-sig',index=False)
# ヒストグラム
plt.bar(x=dist['Value'], height=dist["Freq"],width=1)
plt.xticks(np.arange(len(dist)),list(dist.index),rotation=15)
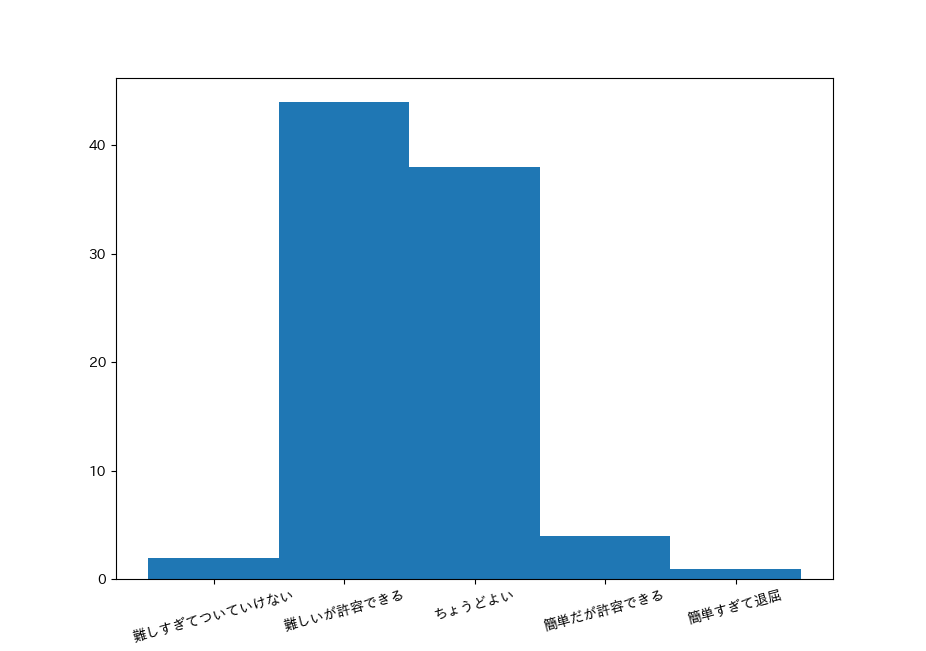
plt.show()以下のように,単峰で右に歪んだグラフが作成されるはずです.
同様に量的データについても作成してみます.
#ヒストグラムを作りたいデータの列名を指定
target_column = 'Values'
# 関数名を sturgesNumber として引数をnとします
def sturgesNumber(n):
# 公式の通り k = 1 + log2 n
# 階級数は整数が良いので,math.floor()で小数点以下を切り捨てます
return (math.floor (1 + math.log2(n)))
# dataフォルダにあるhistogram_quantitative.csvというファイルを読み込みます.
df = pd.read_csv("data/histogram_quantitative.csv")
# 読み込んだファイルの中身を見てみます.
print(df)
#階級数を決定
stnum = sturgesNumber(len(df[target_column]))
print('sturges number:',stnum)
#階級幅を決定
space = int((df[target_column].max() - df[target_column].min()) / stnum)
print('space:',space)
#階級幅の終端を指定
bins = np.arange(start = int(df[target_column].min()) - 1 #最小値
,stop = int(df[target_column].max()) + 1 #最大値
,step = space #階級幅
)
print('bins:',bins)
"""
階級が整数では大きすぎる場合は,
np.arrange()では上手く出来ません.
while文などで,以下のように自作しましょう.
space = (data.max() - data.min()) / step
current = data.min() -1
bins = [current]
while current <= data.max() +1:
current += space
bins.append(current)
"""
#度数
freq = df[target_column].value_counts(bins =bins, sort=False)
print('度数',freq)
rel_freq = freq / df[target_column].count() # 相対度数
cum_freq = freq.cumsum() # 累積度数
rel_cum_freq = rel_freq.cumsum() # 相対累積度数
dist = pd.DataFrame(
{ "Value": freq.index, #階級値
"Freq": freq, #度数
"Rel": rel_freq, #相対度数
"Cum": cum_freq, #累積度数
"RelCum": rel_cum_freq, #相対累積度数
},
index=freq.index
)
print(dist)
dist.to_csv('frequency_table_qualitative.csv'
,encoding='utf-8-sig',index=False)
# ヒストグラム
## dist['Value']は文字列でないので,
## .astype(str) で文字列に変換しています.
plt.bar(x=dist['Value'].astype(str)
,height=dist["Freq"],width=1)
plt.xticks(np.arange(len(dist)),list(dist.index),rotation=15)
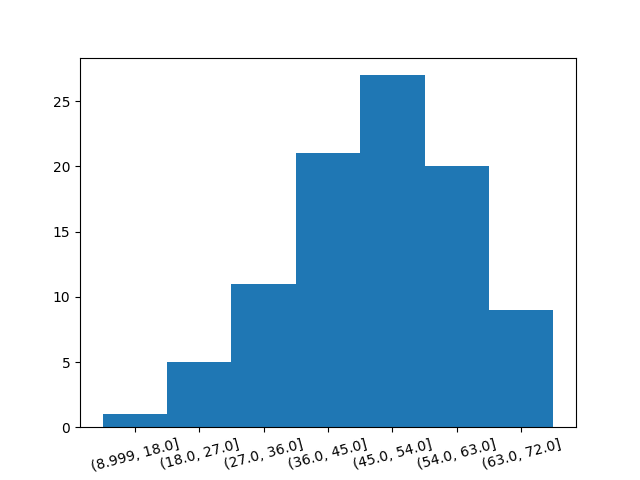
plt.show()以下のように単峰で左に歪んだヒストグラムが作成されます.
一方で,量的データに関しては,度数分布表を作成せずともmatplotlibのplt.hist()を利用して直接作成することも可能です.
plt.hist()ではbins=に階級数を指定することで,その階級数で自然に分割したヒストグラムを作成してくれます.
# ヒストグラムの作成
label = df.columns[0]
values = df[label]
plt.hist(values, bins=stnum)
plt.show()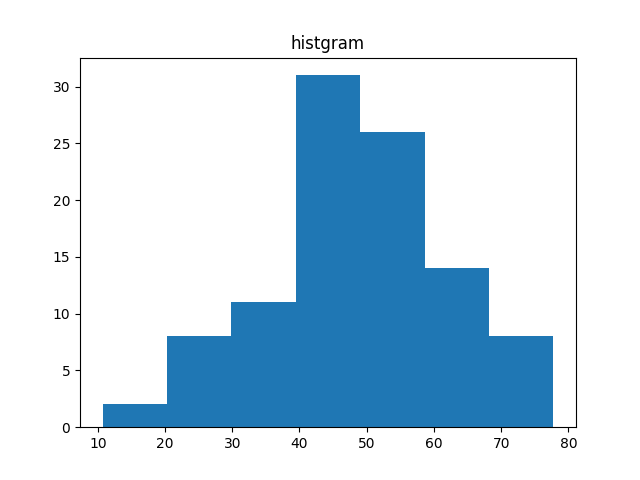
階級幅の設定によって,見た目が変わることが分かります. 作成手法や階級の設定は目的に応じて,使い分けるようにしましょう.
1.6 箱ひげ図
データの観測対象が複数のグループに層別可能な場合には, それぞれのヒストグラムを作成して比較することなどが必要です. グループの数が多い場合には, 何個もヒストグラムを作成することになりますし,比較には剥いていない場合があります. そのような複数のグループの分布を比較する際に良く用いられるグラフが,箱ひげ図です.
こちらのデータは, 複数の種類の馬鈴薯のサイズがまとまっています.
試しに,ヒストグラム馬鈴薯の種類毎のヒストグラムを作成してみます.
df = pd.read_csv('data/boxplot_data_300.csv')
#馬鈴薯の種類を抜き出す
types = list(set(df['Type']))
print(types)
#馬鈴薯の種類別にヒストグラムを作成してみる
fig, ax = plt.subplots(ncols=2
,nrows=int(len(types) / 2) + 1
,sharex = True)
axes = ax.flatten()
fig.suptitle('Potato Weight')
for i in range(len(types)):
t = types[i]
df_temp = df[df['Type'] == t]
axes[i].hist(df_temp['Weight'])
axes[i].set_title(t)
plt.show()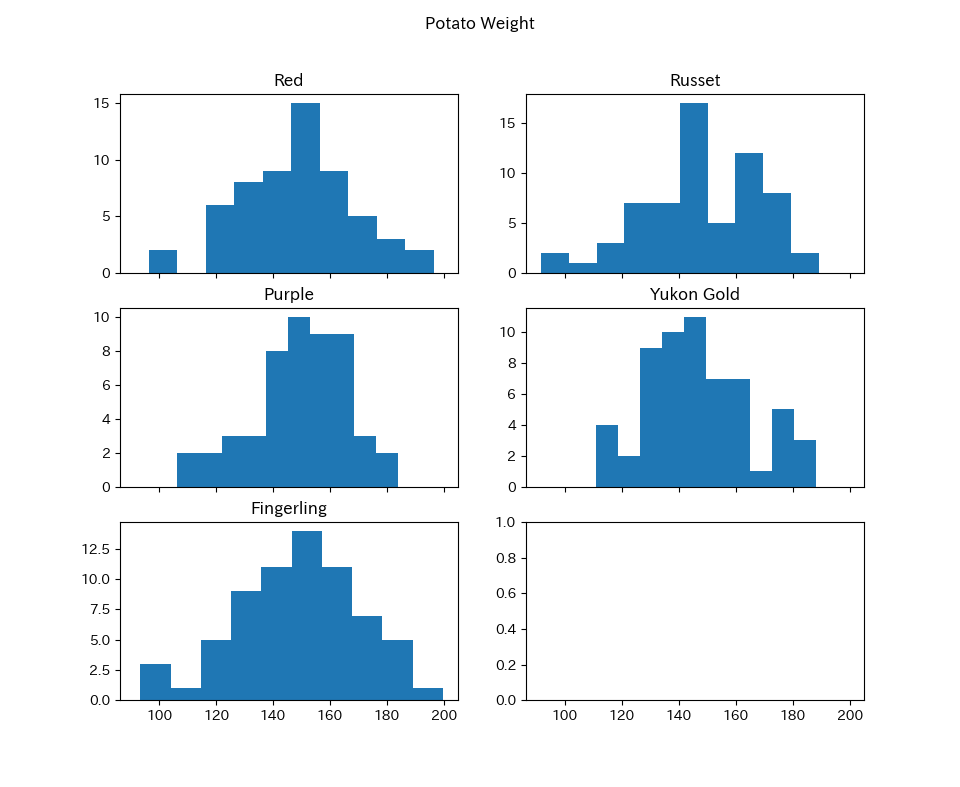
これでも比較はできますが1枚の画像にまとめる手段として,箱ひげ図が利用できます.
箱ひげ図はplt.boxplot(データのリスト,labels=ラベルのリスト)で生成できます.
data = [df[df['Type']==x]['Weight'] for x in types]
"""
#内包表記を利用しない場合は
data = []
for x in types:
data.append(df[df['Type']==x]['Weight'])
"""
print(data)
plt.boxplot(data,labels=types)
plt.show()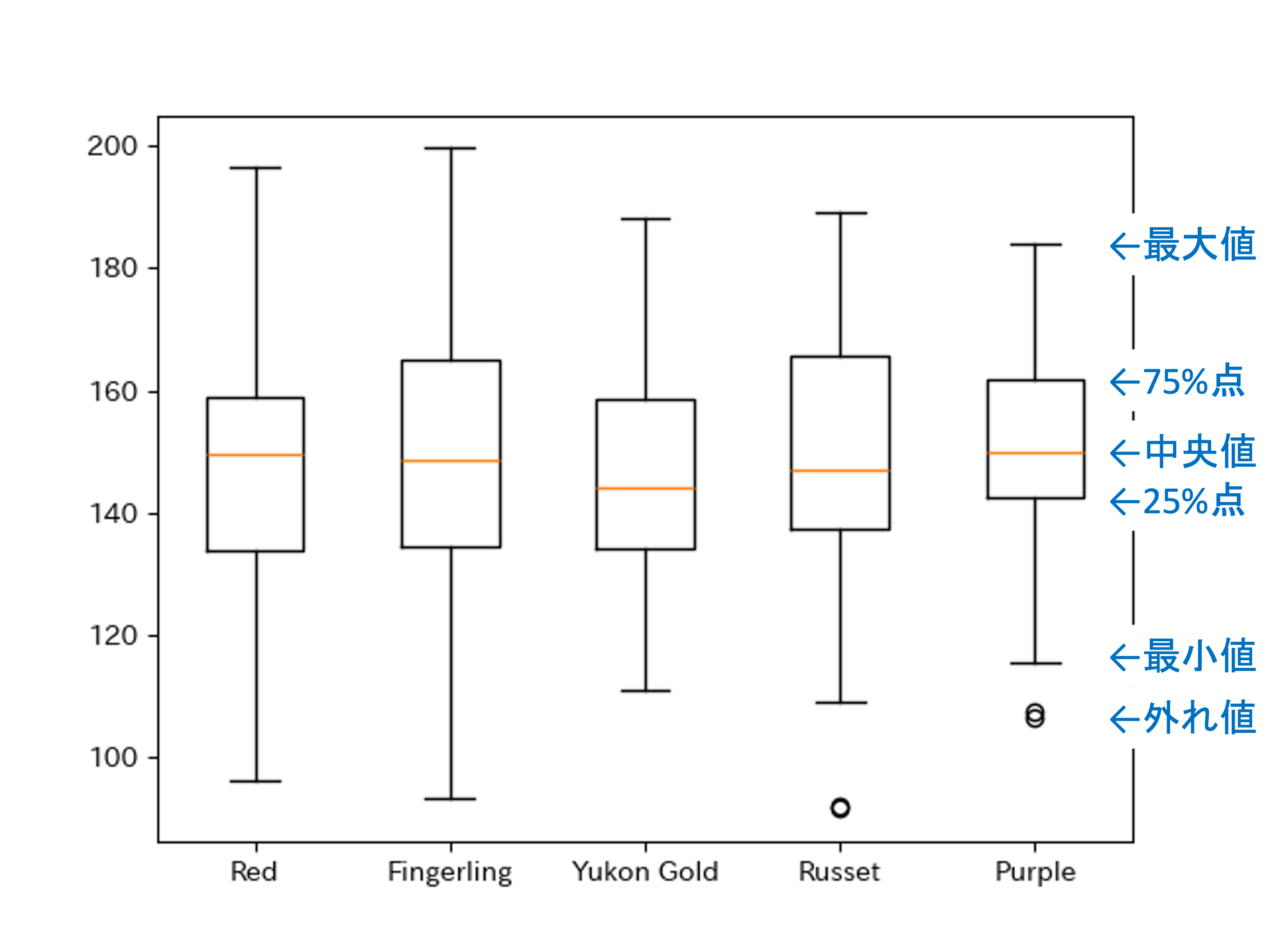
箱ひげ図は,線がそれぞれ四分位数を表しており,それぞれ上から最大値,75%点,中央値,25%点,最小値となります.また,外れ値は丸で表されます.
ヒストグラムと比較して情報量は減りますが, 一覧性と比較においては優れています.それぞれ一長一短なので,用途に応じて使い分けるようにしましょう.
1.7 発展:密度プロット
データの分布を表現する手法としてヒストグラムは非常に便利ですが,階級数や階級幅を自分で定める必要があり,その設定によって見た目が変わってしまいます. また, データ数が少ないときには正確なデータの分布をつかめないという問題点もあります.
そこで, データを階級で区分せずに,度数ではなく確率分布を直接推定する手法にカーネル密度推定(Karnel Density Estimation)があります.
1.8 発展:sinaplot
1.9 発展:バイオリンプロット
1.10 散布図
これまではデータの各観測項目を独立に可視化してきました. 複数の観測項目の関係性を可視化する代表的な手法に散布図があります.
こちらのデータはGoogle Trendにおける同時期のAIというワードのの検索量と,Pythonというワードの検索量を表しています.
AI Python
0 34 27
1 40 26
2 59 28
3 46 29
4 36 29
.. .. ...
255 58 83
256 69 87
257 59 82
258 62 84
259 59 87この2つの検索量がどのような関係にあるのかを散布図を用いて確認してみましょう.
散布図はplt.scatter(x軸の値のリスト,y軸の値のリスト)の形で作成できます.
df = pd.read_csv('data/scatter.csv')
#散布図のx軸を指定
x_column = 'AI'
#散布図のy軸を指定
y_column = 'Python'
x_value = df[x_column]
y_value = df[y_column]
plt.scatter(x_value, y_value)
plt.ylabel(y_column)
plt.xlabel(x_column)
plt.show()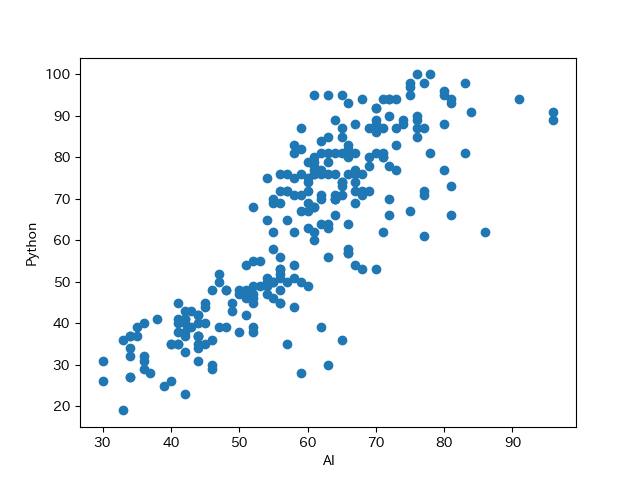
散布図を見ると,AIに関する検索量が増えるにつれて,Pythonの検索量が増えるという関係が見えてきます.
この関係の度合いを数値化する相関係数や,関係の仕方を説明する回帰分析に関しては後ほど扱います.
1.10.1 観測項目が複数ある場合の散布図
データが3つある場合には,以下のように3Dで表現することも可能ですがこの講義では,3次元のグラフに関しては深く扱いません.興味のある方は調べてみましょう.
x = np.random.rand(100)
y = np.random.rand(100)
z = np.random.rand(100)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(x, y, z, color='blue')
plt.show()
plt.close()
観測項目が4つ以上ある場合に散布図のように関係を表す手法としては,複数の観測項目の値を合成して3次元以下にする次元削減が良く利用されます. 次元削減に関しては後ほど扱うとして,ここではいくつかの観測項目を色や大きさなどの要素の変換して関係を見る方法を紹介します.
plt.scatter()ではs=に数値を与えることでサイズ,c=に数値を与えることで色を指定できます.
また,色と数値の関係はplt.colorbar()で表示可能です.
複数の点が重なると見にくくなるために alpha=に0-1の間の数値を指定して透明度を指定することができます.
x = np.random.rand(100)
y = np.random.rand(100)
z = np.random.rand(100)
#色とサイズをzで指定する
#そのままだとサイズが小さすぎるので,100倍している
plt.scatter(x,y,alpha=0.5,s=z*100,c=z)
plt.colorbar() #カラーバーの表示
plt.show()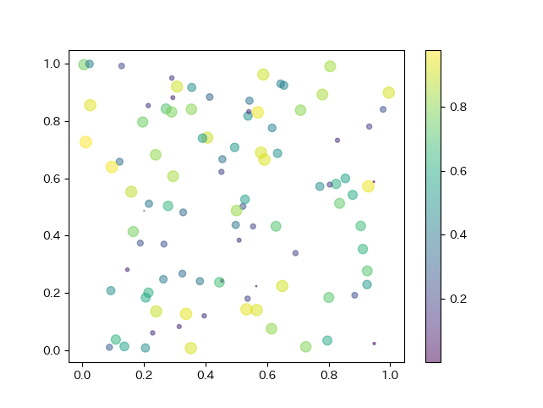
1.10.2 クラスタリングにおける散布図
散布図は複数の観測項目間の関係性を可視化するための手法ですが,データから特定の観測対象の集まり(クラスター)を発見するクラスタリングとも深い関わりがあります. クラスタリングの手法は後ほど扱いますが,ここでは可視化手法としての散布図とクラスタ表現の関係に関して確認してみましょう.
こちらのデータはクラスタリングによって得られたクラスタ毎のラベルがなされています.
x y Cluster
0 -8.149818 -9.152380 2
1 5.860155 0.126873 1
2 -3.213409 9.828126 0
3 6.744070 -0.129607 1
4 -6.342946 -6.038933 2
.. ... ... ...
95 -3.524581 9.931801 0
96 -0.962698 10.411206 0
97 4.397950 2.579246 1
98 -5.255050 -5.299407 2
99 -3.768024 8.550468 0クラスタを表現は.scatter(color=)で色を指定することが一般的です.
#散布図をクラスタごとに色を変えて表示
for i in range(3):
df_temp= df[df['Cluster'] == i]
plt.scatter(df_temp['x']
,df_temp['y']
,c=color_list[i]
,label='Cluster:' + str(i))
plt.legend()
plt.show()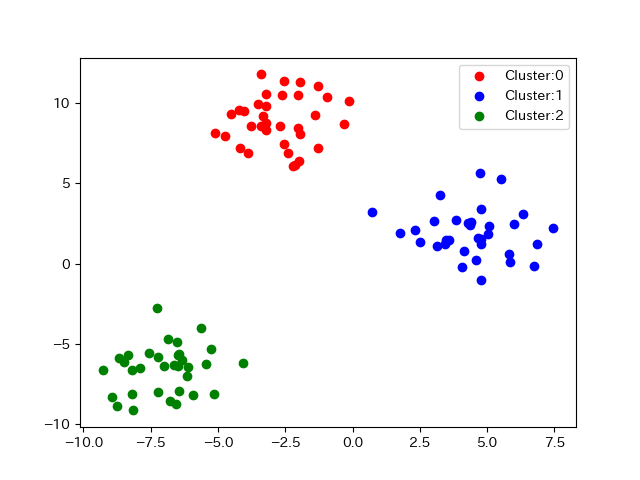
1.11 同時度数分布表
2つの観測項目の関係を調べる手法として散布図を学びましたが,散布図は量的データにしか使えません. 質的変数同士の関係性を調べるにはどのようにしたらいいのでしょうか.
質的変数同士の関係性を調べる手法として代表的なものに同時度数分布表(クロス表)があります. 例えばこちらのデータはある講義の成績情報ですが,観測項目として成績以外に1時限から5時限までの時限が記録されています. 時限が早い講義と遅い講義で成績が変わるのかという関係性を調べてみます.
Period Grade
0 2 B
1 5 A
2 4 A
3 3 C
4 1 C
.. ... ...
195 2 C
196 4 C
197 5 C
198 5 F
199 4 C試しに,散布図でPeriodとGradeの関係を表してみましょう.
成績をそのままでは,散布図の軸上に配置できないので数値に変換します.
df = pd.read_csv('data/cross_table_data.csv')
print(df)
#あえて散布図を作ってみる
grade_num_map = {'S':1
,'A':2
,'B':3
,'C':4
,'F':5}
df['Grade_num'] = df['Grade'].map(lambda x: grade_num_map[x])
plt.scatter(df['Period'],df['Grade'])
plt.xlabel('Period')
plt.ylabel('Grade')
plt.show()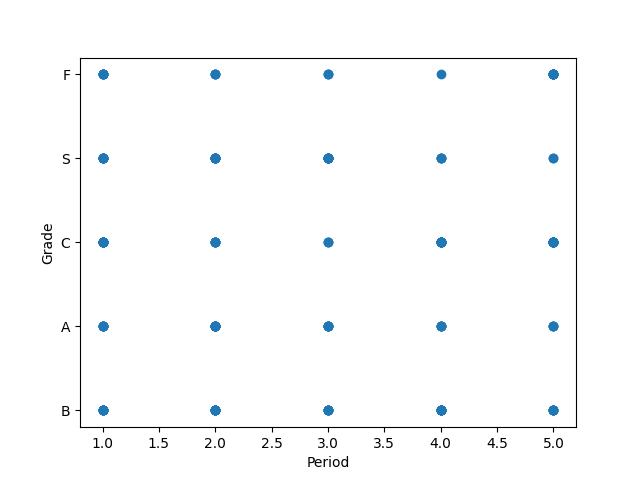
質的データを数値に変換したとしても,離散値となるため,散布図はこのように基本的にはすべての交点に点があるだけのなんの情報も得られないグラフとなります.
散布図としてプロットすると, 点がありうる場所が少なすぎるため情報がとれません. 元々知りたいことは,講義の時限と成績にどのような関係があるのかということでした. そこで, 講義の時間ごとの成績の偏りが分かるように可視化することを考えてみます.
講義の時限ごとの成績の分布がわかり,それぞれに違いがあれば時限によって成績に偏りが出ていると言えそうです. そこで,以下のように講義の時限毎の成績の度数分布表を作ってみましょう.
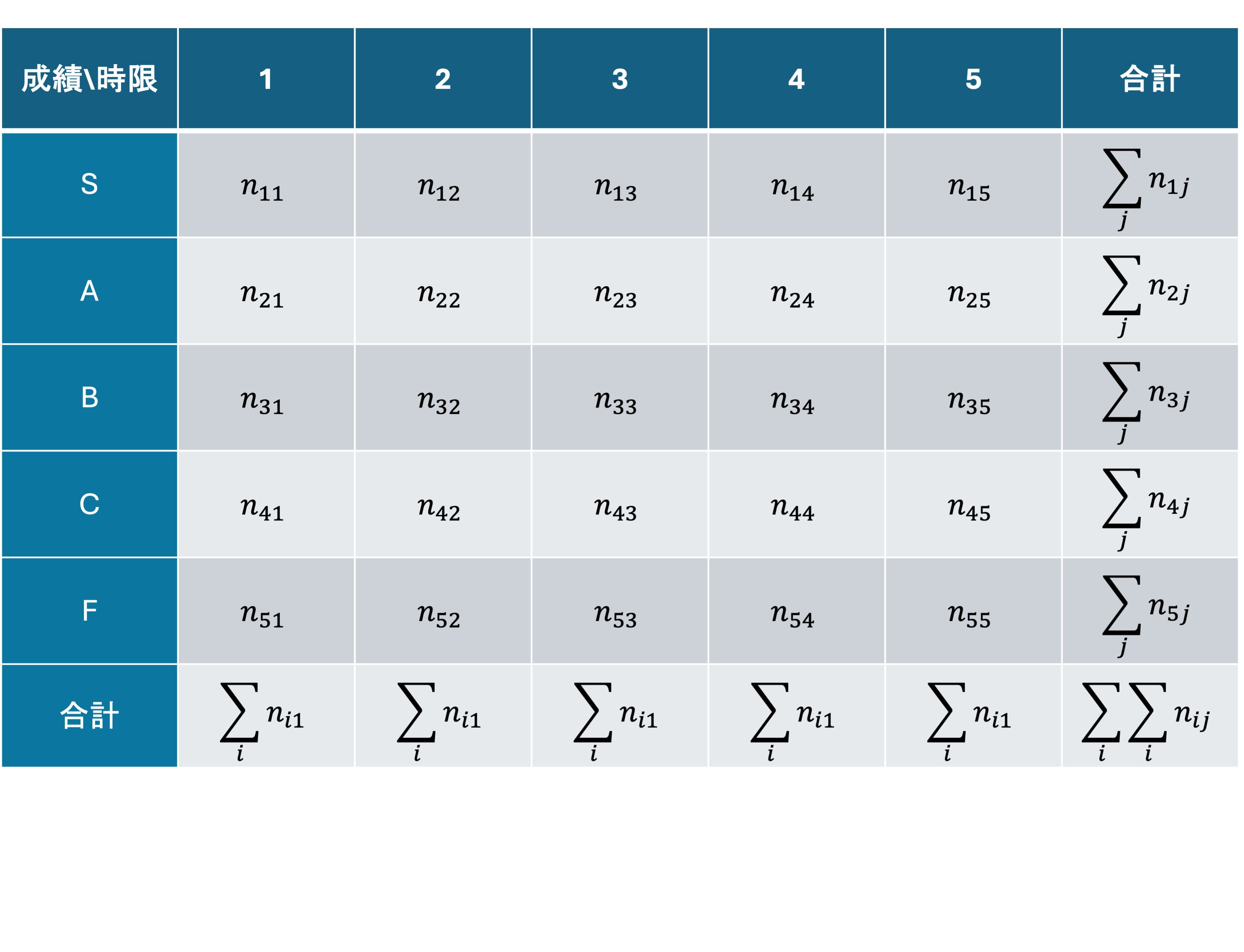
この度数分布表では,時限毎にその成績を取った学生の度数が数えられています(n_{11}は1時限にSを取った学生の度数,n_{ij}はj時限に上からi番目の成績をとった学生の度数.)
このような2観測項目の度数分布表を同時度数分布表あるいは,クロス表(cross table)といいます.
それでは,Pythonで同時度数分布表を作成してみましょう.
pandas では,.crosstab(行,列)メソッドを利用することで,クロス表が作成できます.
#クロス表の作成
cross = pd.crosstab(df['Grade'],df['Period'])
#表示順の設定
cross = cross.reindex([1,2,3,4,5],axis='columns')
cross = cross.reindex(['S','A','B','C','F'],axis='index')
print(cross)Period 1 2 3 4 5
Grade
S 9 10 12 4 2
A 7 14 7 5 4
B 9 10 7 11 7
C 14 6 3 15 18
F 7 4 3 1 11このようにしてみることで,それぞれの時限毎にそれぞれの成績がどのような分布なのかが分かります. しかし,各時限の人数が同じとは限らないため,各列の値をその列の和で割って,列相対度数に変更してみましょう.
#列相対度数に変更する
for c in cross.columns:
cross[c] = cross[c] / cross[c].sum()
print(cross)Period 1 2 3 4 5
Grade
S 0.195652 0.227273 0.37500 0.111111 0.047619
A 0.152174 0.318182 0.21875 0.138889 0.095238
B 0.195652 0.227273 0.21875 0.305556 0.166667
C 0.304348 0.136364 0.09375 0.416667 0.428571
F 0.152174 0.090909 0.09375 0.027778 0.261905このようにすると,時限毎にどの程度の割合がSやAなどの良い成績をとっているのかが分かります. 通常度数分布表を作成したあとには,χ二乗検定や,標準化残渣を利用した残渣分析によって,偏りが統計的に存在するかを判定します. しかし,それらは後の検定の章に譲るとして,次の節では更に,これを一目で判断しやすいように可視化することを考えてみます.
1.12 ヒートマップ
一つ前の節では,同時度数分布表を利用して2つの質的変数からなる観測項目の関係性を見てみました. しかし, 同時度数分布表のままでは,可視化とは言えません. 同時度数分布表のような表形式の数値を可視化する方法として,ヒートマップがあります.
ヒートマップとは,表形式の数値を各セルの色によって表現する可視化手法です.
先ほど作成した,列相対度数をヒートマップを利用して可視化してみましょう.
ヒートマップはseabornの.heatmap()を利用することで簡単に作成できます.
sns.heatmap( cross #ヒートマップを作成したいテーブル
, cmap=plt.get_cmap('Reds') #カラーマップ(省略可)
, linewidths=.5 #線の太さを指定することでセルを囲う線を表示
, annot=True #セルに数値を表示
)
plt.show()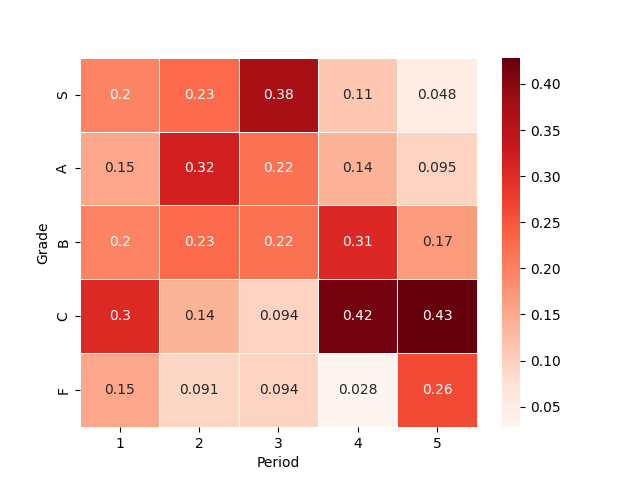
このヒートマップでは,数値が大きいほど,色が濃くなっており2,3時限においてB以上の成績を取る学生の割合が大きいこと,4,5時限においてCやFなどの成績を取る人の割合が大きいことが視覚的に分かります.
ヒートマップは複数の数値間の相関係数や距離を可視化する際にも良く用いられるので,覚えておきましょう.