特別講義DS Ch9 データの数値化
1 データの数値化
データを可視化することで,データの大まかな傾向はつかめます. しかし,グラフではデータの特徴を大まかにしか捉えることが出来ません. 実際に,データの特徴に関して言及するためにはそれを数値にする必要があります.
例えば,以下のヒストグラム(データ)を見てみましょう.
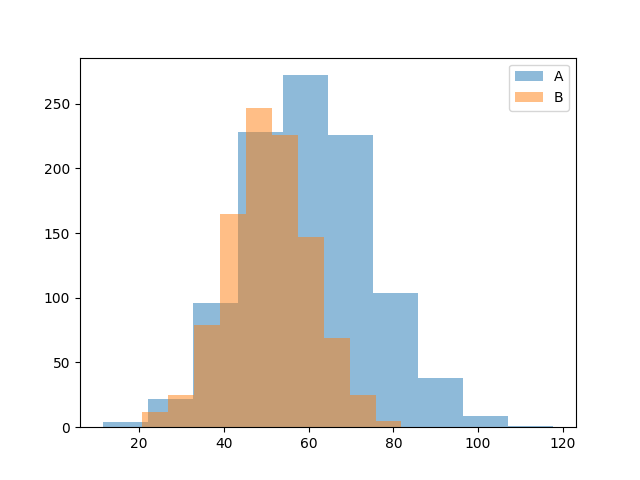
ヒストグラムAと比較して,Bはデータの中心が右にあり,データの散らばりが大きいように見えます. しかし,それらが具体的にどの程度右にあり,どの程度散らばりが大きいのでしょうか. このように,グラフによる比較では,抽象的な印象しか語ることができないため,データの中心や,散らばりを数値で表すことが必要です.
数値化の対象となる量は,データの種類や分析の目的によって様々ですが,大まかに以下のような分類が可能です.
データの数値化
| データの数 | データの種類 | 求める数値 | 目的 |
|---|---|---|---|
| 1 | 量的変数 | 基本統計量 | データの特徴を知る |
| 2 | 量的変数 | ピアソンの積率相関係数 | データの関係を知る |
| 2 | 質的変数 | ピアソンのΧ二乗統計量 スピアマンの順位相関係数 |
データの関係を知る |
| 2 | 混在 | 寄与率,相関比 | データの関係を知る |
| 3以上 | 次元削減,多変量解析など多数 |
1.1 基本統計量
量的データを客観的に評価するために,分布の特徴を数値で表したものを基本統計量(代表値)といいます.
- 基本統計量
| 名称 | 概要 |
|---|---|
| 平均 (Mean) | データの平均値.量的データの分布の中心傾向を示す |
| 中央値 (Median) | データの順位における中央.量的データの分布の中心傾向を示す |
| 最頻値 (Mode) | 最も度数の多い値.量的データの分布の中心傾向を示す |
| 標準偏差 (Standard Deviation) | データのばらつき具合を示す. |
| 分散 (Variance) | データのばらつき具合を示す. |
| 尖度 (Kurtosis) | 外れ値の度合い |
| 歪度 (Skewness) | 分布の歪み |
Pythonでは, pandasのDataFrameに対して, .describe()メソッドを適用すると, データ数(count),平均値(mean),中央値(50%),四分位数(24%,75%),標準偏差(std),最大値(max),最小値(min)などが求まります.
df = pd.read_csv('data/histogram_A_B_data.csv')
print(df.describe())
"""
python quantify.py
Histogram_A Histogram_B
count 1000.000000 1000.000000
mean 60.289981 50.708362
std 14.688239 9.974544
min 11.380990 20.596114
25% 50.286145 43.937583
50% 60.379509 50.630771
75% 69.719158 57.288822
max 117.790972 81.931076
"""それぞれの統計量の意味を順番に見ていきましょう.
1.2 中心を表す基本統計量
ヒストグラムにおける峰のある位置,分布の中心がどこにあるかを表す統計量には,平均値,中央値,最頻値などがあります. この3つは,いずれも分布の中心を表す統計量ですが,分布の歪みによって意味が異なり,使い分けが必要となります.
算術平均 (mean)
分布の中心を表す統計量としてもっとも一般的なものに,平均値があります. しかし, 一言に平均といっても,いくつかの種類があるので注意しましょう. 分布の中心を表す場合に用いられる平均は基本的に算術平均ですが, ここでは異なる定義の平均として, 幾何平均と調和平均も紹介します.
一般に「平均」といった時にイメージされる,すべてのデータの和をデータの個数で割った値を算術平均といいます.
算術平均は対象とするデータを足し合わせることによって基準となる値が算出される場合に使用します.
n個の観測値 $ x_1, x_2, …, x_n $ の時,平均値 $ {x} $ は
\bar{x} = \frac{1}{n} (x_1 + ... + x_n) = \frac{1}{n} \sum_{i=1}^{n} x_i
例: 165,171,189の算術平均は
\bar{x} = \frac{1}{3} (165 + 171 + 189) = 175
となります.
pandasで平均を求めるには, .mean()を利用します.
df = pd.DataFrame({'x':[165,171,189]})
print(df['x'].mean()) #>>>175幾何平均(geometric mean)
すべてのデータを乗じて,データの数で根を取った値を幾何平均といいます. 増加率,減少率など対象とするデータを相互に乗じることによって基準となる値が算出される場合に使用します.
n個の観測値 x_1, x_2, ..., x_n の時,幾何平均 x_G は x_G = \sqrt[n]{x_1 \cdot x_2 \cdot ... \cdot x_n} = (\prod_{i}^{n} x_i)^{\frac{1}{n}}
例:各年の売上と,その増加率が以下のように表されるとき,平均何%売上が伸びているかを考える.
| 年度 | 売上 | 増加率 |
|---|---|---|
| 1 | 300 | |
| 2 | 350 | 117% |
| 3 | 600 | 171% |
| 4 | 1000 | 167% |
このとき算術平均を用いると, 算術平均 = \frac{1.17 + 1.71 + 1.67}{3} \approx 1.52 となり,
300 \cdot 1.52^3 \approx 1045
平均的な伸び率を3回乗じても4年目の売上の値になりません. これは,毎年度の値に増加率を掛けることで次の年度の値が求まるのに対して,算術平均は毎年度足す操作をしたばあいの平均値を求めているからです.
そこで,幾何平均を求めてみると.
幾何平均 = \sqrt[3]{1.17 \cdot 1.71 \cdot 1.67} \approx 1.49, \\ 300 \cdot 1.49^3 \approx 1000 となり, 正確に4年目の値が計算できていることが分かります.
調和平均(harmonic mean)
先程の幾何平均が掛け算の平均値だったのに対して,割り算の平均値を調和平均といい,速度などの定義に割り算が含まれている計算で用います.
調和平均は対象とするデータに別の値を除して足し合わせることによって基準となる値が算出される場合に使用します.
n個の観測値 x_1, x_2, ..., x_n の時,調和平均 x_H は \frac{1}{x_H} = \frac{1}{n} \left( \frac{1}{x_1} + ... + \frac{1}{x_n} \right) \\ \iff \\ x_H = \frac{n}{\frac{1}{x_1} + ... + \frac{1}{x_n}} = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}}
例:平均速度
100kmの道のりを行きは車 (60km/h),帰りは自転車 (30km/h) で移動した場合,算術平均は 45km/hとなります. しかし,
かかった時間は \frac{距離}{速度}で求まるので, 車は \frac{100}{60}, 自転車 は \frac{100}{30} となり,速度は \frac{距離}{時間} で求まるので
平均速度は, \frac{200}{\frac{200}{60} + \frac{200}{30}} = \frac{2}{\frac{1}{30} + \frac{1}{60}} = 40
となります. 算術平均では正確に計算できていないことが分かります.
この \frac{200}{\frac{200}{60} + \frac{200}{30}} が調和平均です.
中央値(median)
中心を表す統計量として,データを昇順に並び替えて,そのちょうど真ん中の数を表す中央値も良く利用されます.
n個の観測値を大きさの順に並べ替えて x_1, x_2, ..., x_n とした時, 中央値 \tilde{x} は
\tilde{x} = \begin{cases} x_{\frac{n+1}{2}}, ~~& if ~~ n \mod 2 \neq 0 \\ \frac{x_{ \frac{n}{2}} + x_{\frac{n}{2} + 1 }}{2}, ~~ & if~~ n \mod 2 = 0 \end{cases}
例:観測値が 3, 4, 7, 9, 11, 12, 15 の時 中央値は \tilde{x} = x_{\frac{n+1}{2}} = x_{\frac{8}{2}} = x_4 = 9
となります.
また,観測値が 4, 5, 6, 10, 14, 17 のように偶数個の場合は \tilde{x} = \frac{x_{ \frac{n}{2}} + x_{\frac{n}{2} + 1 }}{2} = \frac{6 + 10}{2} = 8
となります.
pandasでは,中央値は.median()で求めることができます.
df = pd.DataFrame({'x':[3,4,7,9,11,12,15]})
print(df['x'].median()) #9.0
df = pd.DataFrame({'x':[4,5,6,10,14,17]})
print(df['x'].median()) #8.0四分位数 (quartiles)
中央値: データを小さい順に並べた時に観測数が50%となる点
四分位数: データを小さい順に並べた時に,観測数が25%, 50%, 75%となる点. 第一四分位数 (25%),第二四分位数 (50%),第三四分位数 (75%)
四分位範囲: 四分位範囲 = 第一四分位数から第三四分位数の範囲

pandasで四分位数を用いるには, .quantile(q=%点の数値,interpolation='nearest')で求めることができます.
interpolation (補間) は,値がインデックスiとjの間にある場合に補間する方法を指定する引数で以下のような設定が可能です.
.quantile()では, データの最大インデックス掛けるqで必要な値を求めます. なので例えばxs=[2,5,8,9,11,13,15,16,19,22,24]の25%点は,10*0.25=2.5となりxs[2.5]となるような点を求めます.
| 引数 | 効果 | 25%点の場合の計算 |
|---|---|---|
'linear' |
線形補間 | xs[2] + (xs[2] - xs[3]) * 0.5 = 8.5 |
'lower' |
小さい方 | xs[2] = 8 |
'higher' |
大きい方 | xs[3] = 9 |
'midpoint' |
中間 | (xs[2] + xs[3])/2 = 8.5 |
'nearest' |
近い方 | xs[2] = 8 |
xs = [2,5,8,9,11,13,15,16,19,22,24]
df = pd.DataFrame({'x':xs})
print('25%点:',df['x'].quantile(q=0.25, interpolation='linear'))
print('25%点:',df['x'].quantile(q=0.25, interpolation='nearest'))
print('50%点:',df['x'].quantile(q=0.5, interpolation='nearest'))
print('75%点:',df['x'].quantile(q=0.75, interpolation='nearest'))
"""
25%点: 8.5
25%点: 8
50%点: 13
75%点: 19
"""最頻値 (mode)
中心を表す統計量の最後は,最も頻繁にあらわれる値,すなわち度数分布表において最も度数の高い階級を表す最頻値です.
最頻値はデータの種類に応じて,意味が異なるので注意が必要です. (※ 質的データの平均値などは定義できません)
質的データの場合
- 最大度数のカテゴリー
量的データの場合
最大度数の階級 = 最頻階級 (modal class)
長さや気温など同じ間隔で値が存在するもの
pandasで最頻値を求める方法は色々ありますが, 単純に同じデータが最も多い値を探す場合には.mode()が利用できます. .mode()は最頻値が複数ある場合に対応するためにDataSeriesObjectを返すので,[0]で最初の値を取っています.
df = pd.DataFrame({'x':['A','A','B','C']})
print(df['x'].mode()[0]) # A
df = pd.DataFrame({'x':[1,3,2,4,5,3]})
print(df['x'].mode()[0]) # 3しかし,この方法では連続値の数値などにおける定義での最頻値は求められません. 特定の区間の最頻値を求めたい場合はvalue_count()などを利用して求めましょう.
# ランダムな1から100までのデータの生成
np.random.seed(0) # 再現性のためにシードを設定
df = pd.DataFrame({'x':np.random.randint(0, 101, size=1000)})
print(df)
#10区切りで度数を求める
bins = [0,10,20,30,40,50,60,70,80,90,100]
freq = df['x'].value_counts(bins =bins, sort=False)
print(freq)
#最大の度数のindexを取得
print(freq.idxmax())
"""
x
0 44
1 47
2 64
3 67
4 67
.. ..
995 79
996 41
997 17
998 80
999 43
[1000 rows x 1 columns]
(-0.001, 10.0] 121
(10.0, 20.0] 87
(20.0, 30.0] 96
(30.0, 40.0] 107
(40.0, 50.0] 94
(50.0, 60.0] 92
(60.0, 70.0] 97
(70.0, 80.0] 103
(80.0, 90.0] 103
(90.0, 100.0] 100
Name: count, dtype: int64
(-0.001, 10.0]
"""中心を表す代表値の使い分け
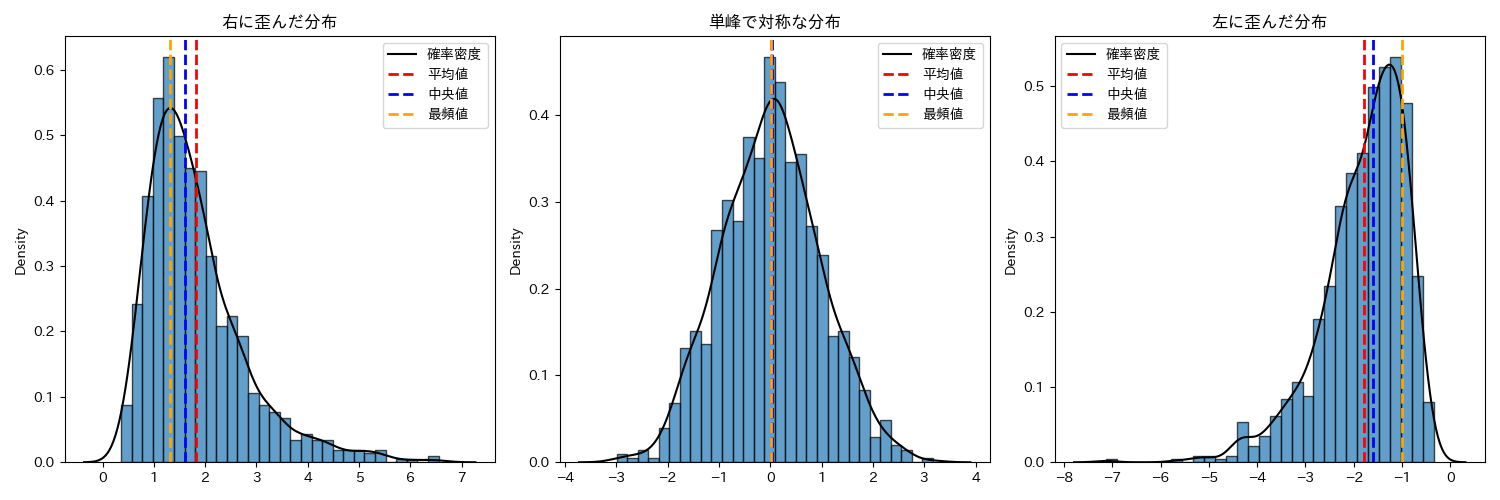
中心を表す基本統計量である,算術平均,中央値,最頻値は,ヒストグラムが単峰で左右対称である場合一致します. したがってヒストグラムを作成して単峰で左右対称である場合には,どの値を利用しても大きな違いは生まれません.
一方で,分布が歪んでいる場合には,それぞれの統計量の値が変わります. 中心を表す統計量として,何も考えずに算術平均を利用する人がいますが,分布が歪んでいる場合には目的に応じて最頻値や中央値の方が適当である場合があります.
例えば,以下の図は,日本人の平均所得を表したヒストグラムです.
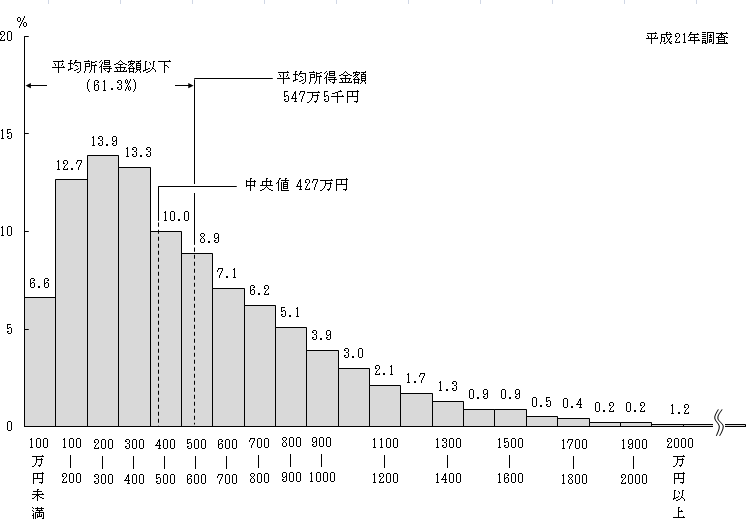
この図では,分布が大きく右に歪んでいるため平均値,中央値,最頻値の値が異なっています.それぞれの値が何を意味するのかを考えてみましょう.
- 平均値: 547万円
- 全員の所得を足して一人あたりで割る(仮に全員平等にもらえるならこの金額)
- 中央値: 427万円
- 下から所得の低い順に並んだときに真ん中の人(これ以上なら真ん中より上の所得)
- 最頻値: 250万円
- 一番多い(街で適当に声をかけるとコレくらいである可能性が高い)
このようなときに, 世間一般の人の感覚を表す値として平均値を利用することは適当ではないでしょう. 平均値は,分布が歪んでいる場合には少数のデータに大きく引っ張られるため全体の傾向を表せない場合があります.
例えば,年収300万円の人が100人いる村に年収50億円の野球選手が引っ越してくると,平均年収は5000万円,中央値,最頻値は300万円になります.
統計量はそれぞれの意味を把握したうえで, 目的に応じて使い分けるようにしましょう.
1.3 データの広がりを表す統計量
分布の中心がどこかという点の他に,データがどのように広がっているかもデータの特徴を記述するうえでは重要です.

データの広がり具合を散布度といいますが,散布度を表す統計量として代表的なものに分散と標準偏差があります.
データの散らばり具合を数値化するために,どのように考えるかを順におって見ましょう. データがどの程度散らばっているかを考える際の基準の一つが算術平均 \bar{x} です. 各データ x_i が,データの算術平均からどの程度離れているのかを考えてみましょう.
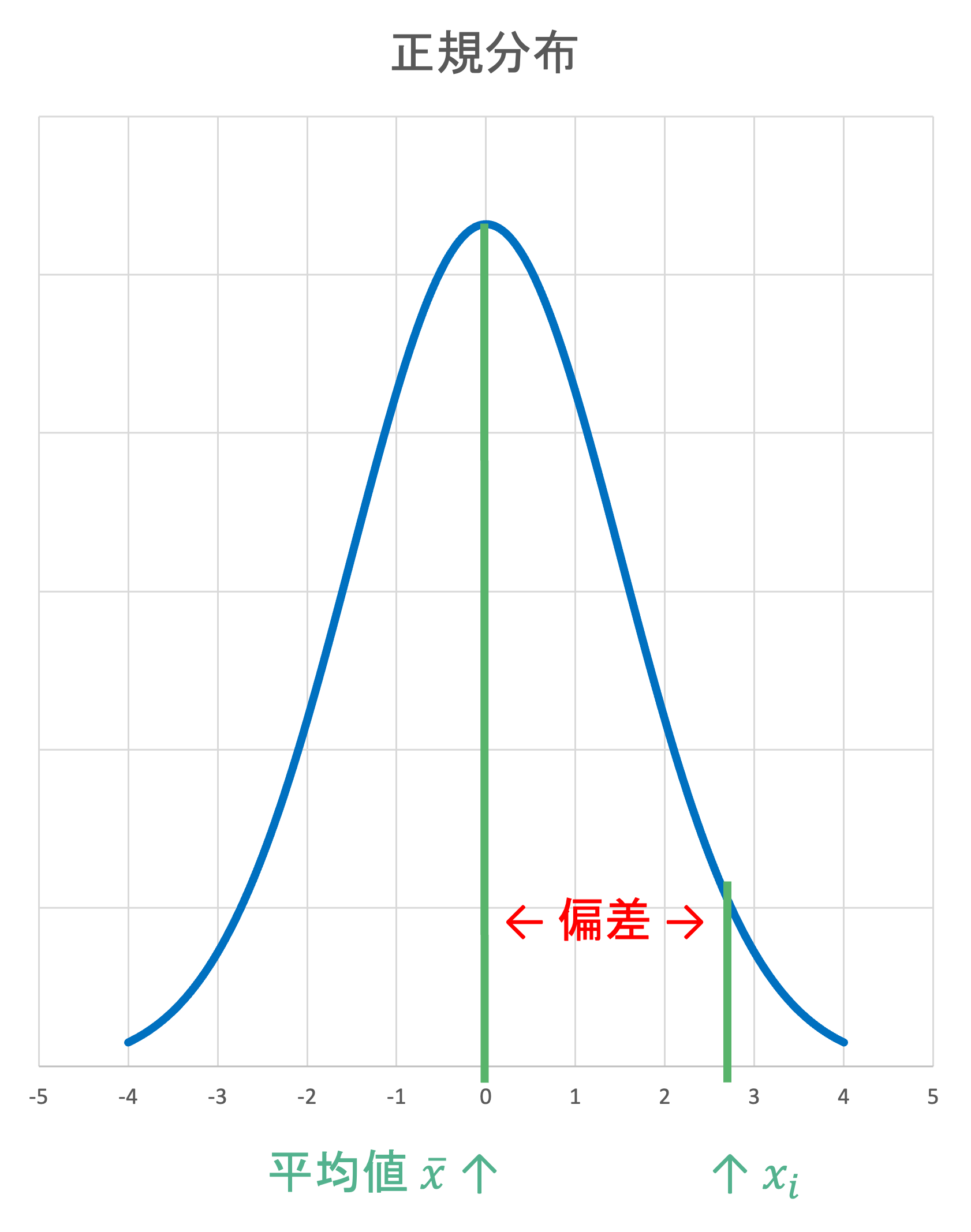
- 偏差(deviation)
\text{観測値} x_i \text{と平均} \bar{x} \text{の差} = x_i - \bar{x}
この偏差がデータ全体でどのくらい大きいのかを考えるために偏差の平均を取ります. ただし,平均からの差は,すべて足し合わせると0になるため,絶対値を取ります.これを平均偏差と呼びます.
- 平均偏差(mean deviation)
各観測値が平均からどれだけ離れているかの絶対値平均
d = \frac{1}{n} \sum_{i=1}^{n} |x_i - \bar{x}|
絶対値の計算は面倒なので,値が大きくはなるけれど2乗してみることにします. これが分散です.
- 分散(variance)
各観測値の偏差の2乗の平均
S^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2
2乗すると値が大きくなるので,単位をもとのデータに合わせるために分散の平方根をとります(例えば, x_i の単位がKgのとき, S^2 の単位は Kg^2 となってしまう).これを標準偏差といいます.
- 標準偏差(standard deviation)
S = \sqrt{S^2}
例えば, データが[9,6,12,18,10]の場合を考えてみましょう. 何を計算しているのか,イメージしながら順番に計算していきましょう.
data = [9,6,12,18,10]
df = pd.DataFrame({'data':data})
print(df)
"""
data
0 9
1 6
2 12
3 18
4 10
"""まずは平均からの差(偏差)を求めてみます.
#平均
barx = df['data'].mean()
print(barx) #11.0
# 偏差
df['dev'] = df['data'] - barx
print(df)
"""
data dev
0 9 -2.0
1 6 -5.0
2 12 1.0
3 18 7.0
4 10 -1.0
"""次に偏差の2乗とその平均(分散)を求めます.
#偏差の2乗
df['dev2'] = df['dev'] * df['dev']
print(df)
"""
data dev dev2
0 9 -2.0 4.0
1 6 -5.0 25.0
2 12 1.0 1.0
3 18 7.0 49.0
4 10 -1.0 1.0
"""
#偏差の2乗の平均(分散)
print(df['dev2'].mean()) #16.0最後に分散の累乗根をとって,標準偏差を求めます.
#偏差の2乗の平均の累乗根(標準偏差)
print(np.sqrt(df['dev2'].mean())) #4.0計算から,このデータの分散は16,標準偏差は4であることが分かりました.
pandasでは,分散は.var(ddof=0),標準偏差は.std(ddof=0)で求めることができます.
print('分散:',df['data'].var(ddof=0)) #16.0
print('標準偏差:',df['data'].std(ddof=0)) #4.0- 不偏分散,不偏標準偏差
.var()と.std()における引数ddof=0とはなんでしょうか.これは,分散を求める際の分母の値から引く数を表しています(引いた後の値を自由度といいます).
デフォルトの値は,ddof=1となっており,
\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 を求めています.
このような分母が n-1となっている分散を不偏分散といいます. 一方で,これまで計算してきた値を標本分散といいます.
不偏分散の意味に関しては, 統計学入門で学習していただくとして,ここでは一言に分散や標準偏差といっても, 細かくは標本分散,不偏分散,母分散などの異なる概念があることに注意しましょう. 特にプログラムにおいて, 分散や標準偏差を求める際には,それがなんの値なのかに注意が必要です. ネット上の記事などにおいても混同していることが多いので, 実際に自分で計算して確かめることをおすすめします.
例えば,pandasにおけるdescribe()で表示されるstdは不偏標準偏差であり,std(ddof=0)の値とは異なります.
print(df['data'].describe())
"""
count 5.000000
mean 11.000000
std 4.472136
min 6.000000
25% 9.000000
50% 10.000000
75% 12.000000
max 18.000000
Name: data, dtype: float64
"""演習
算術平均,幾何平均, 調和平均,標本標準偏差を計算する関数をそれぞれ作成してください.
こちらのデータの列ごとの算術平均,中央値,最頻値,標本分散,標本標準偏差を求めよ
1.4 相関
基本統計量は,一つの観測項目に対する数値化の手法でしたが,可視化における散布図のように,2つの観測項目間の関係を数値で表すことが可能です.
散布図の節で扱った事例についてもう一度考えてみましょう.
AI Python
0 34 27
1 40 26
2 59 28
3 46 29
4 36 29
.. .. ...
255 58 83
256 69 87
257 59 82
258 62 84
259 59 87df = pd.read_csv('data/scatter.csv')
#散布図のx軸を指定
x_column = 'AI'
#散布図のy軸を指定
y_column = 'Python'
x_value = df[x_column]
y_value = df[y_column]
plt.scatter(x_value, y_value)
plt.ylabel(y_column)
plt.xlabel(x_column)
plt.show()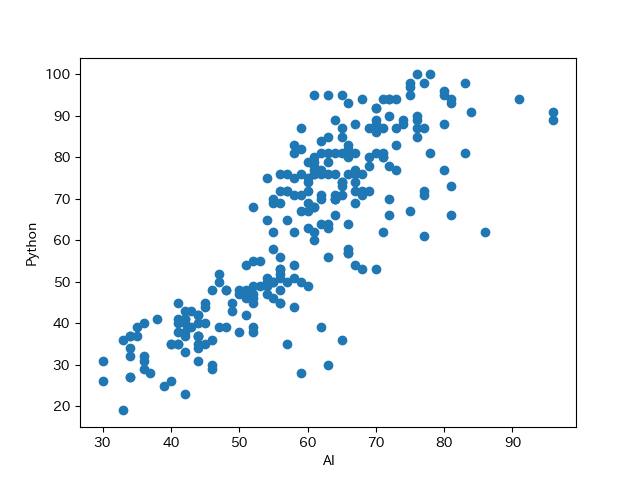
Google Trendの AIとPythonの検索数から散布図を作成すると, AIの検索数が増えるにつれてPythonの検索数が増えていることが分かります.
相関関係
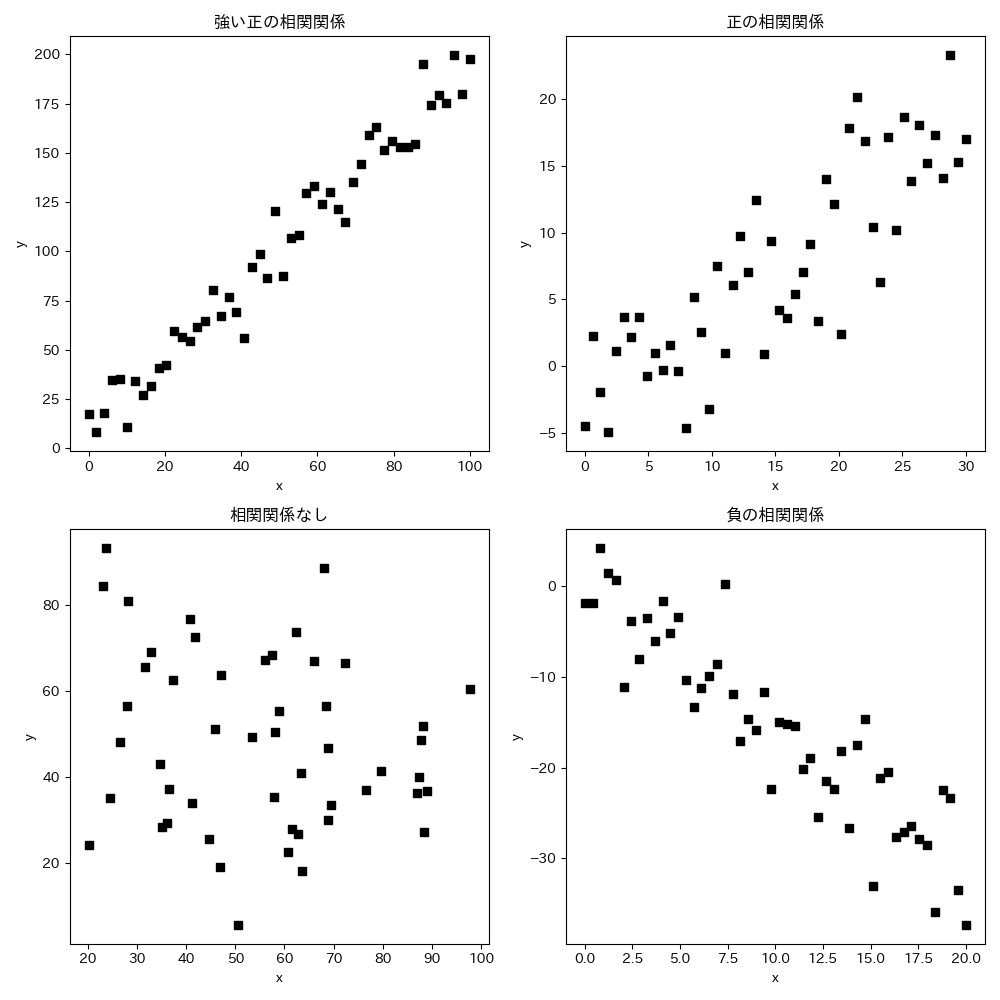
このような関係を相関関係(correlation)といい,2つの変数の間に直線関係に近い傾向が見られるときに「相関関係がある」といいます.
直線的であるほど強い相関,逆を弱い相関といいます.
また,
- 一方が増加したとき,他方が増加する関係を 正の相関関係
- 一方が増加したとき,他方が減少する関係を 負の相関関係
といいます.
このような相関関係があるかないかは,散布図を見ただけである程度判断が可能ですが, 相関がある/ない,強い/弱いというのは抽象的な表現なので, 厳密に判断する場合にはそれらを数値として表す必要があります.
相関関係を数値化したものを相関係数(correlation coefficient)といい,データの尺度に応じて,以下のような種類が存在します.
| 尺度 | 係数 |
|---|---|
| 量的変数 \times 量的変数 | ピアソンの積率相関係数 |
| 順位尺度 \times 順位尺度 | スピアマンの順位相関係数 |
| 名義尺度 \times 質的変数 | ピアソンの \Chi^2 統計量 |
1.4.1 ピアソンの積率相関係数
2つの量的変数に利用される相関係数をピアソンの積率相関係数(product moment correlation coefficient)といいます.
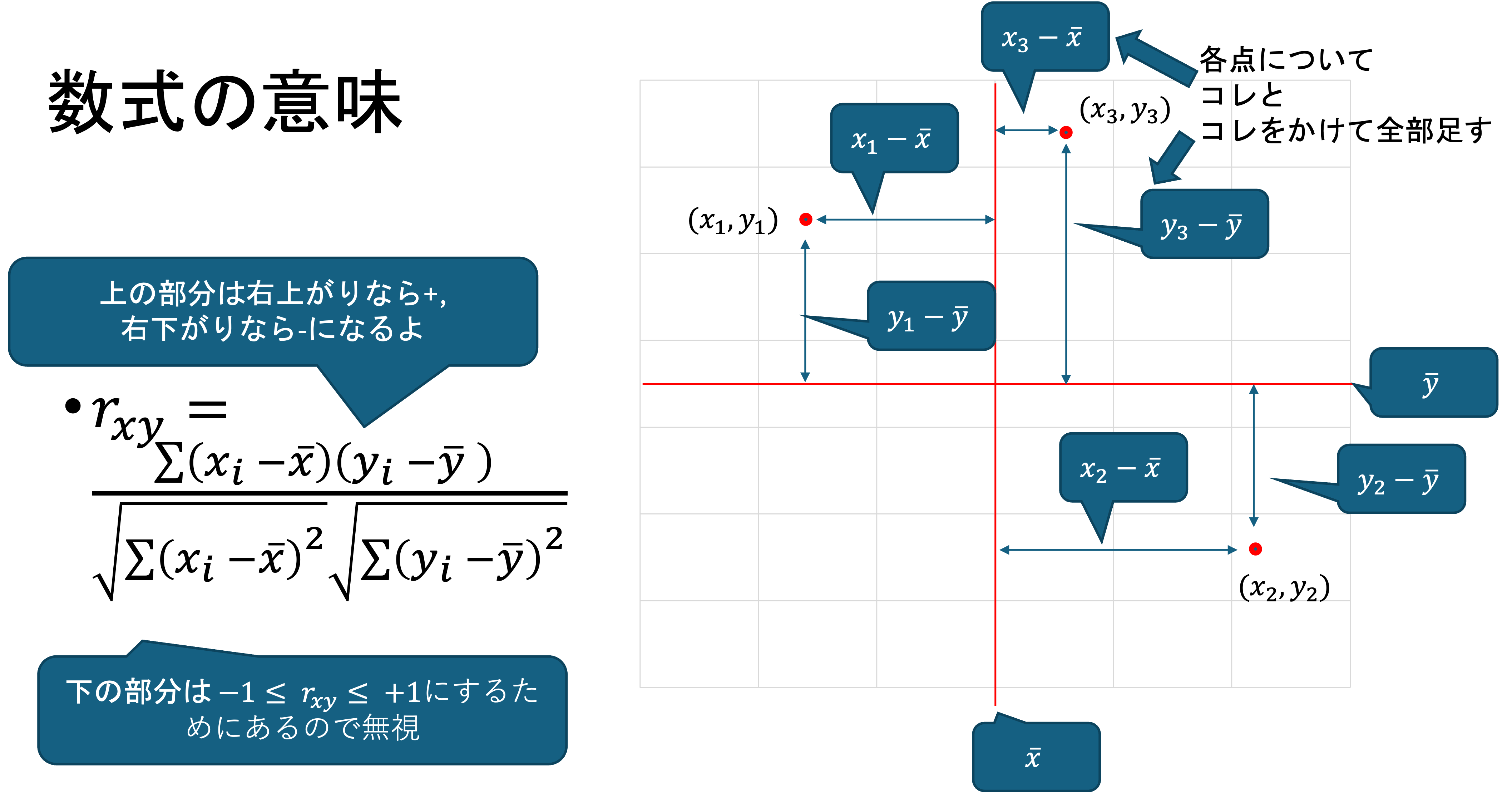
データが (x_1, y_1), (x_2, y_2), ..., (x_n, y_n) の時,
\begin{align*} r_{xy} &= \frac{\sum (x_i - \bar{x})(y_i - \bar{y}) / n}{\sqrt{\sum (x_i - \bar{x})^2 / n} \sqrt{\sum (y_i - \bar{y})^2 / n}} \\ & = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \sqrt{\sum (y_i - \bar{y})^2}} \\ &= \frac{s_{xy}}{s_x s_y} \end{align*}
なお, \quad s_{xy} = \frac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y}) を x と y の共分散といい,相関係数は \frac{xとyの共分散}{xの標準偏差 \times yの標準偏差}の形で表されます.
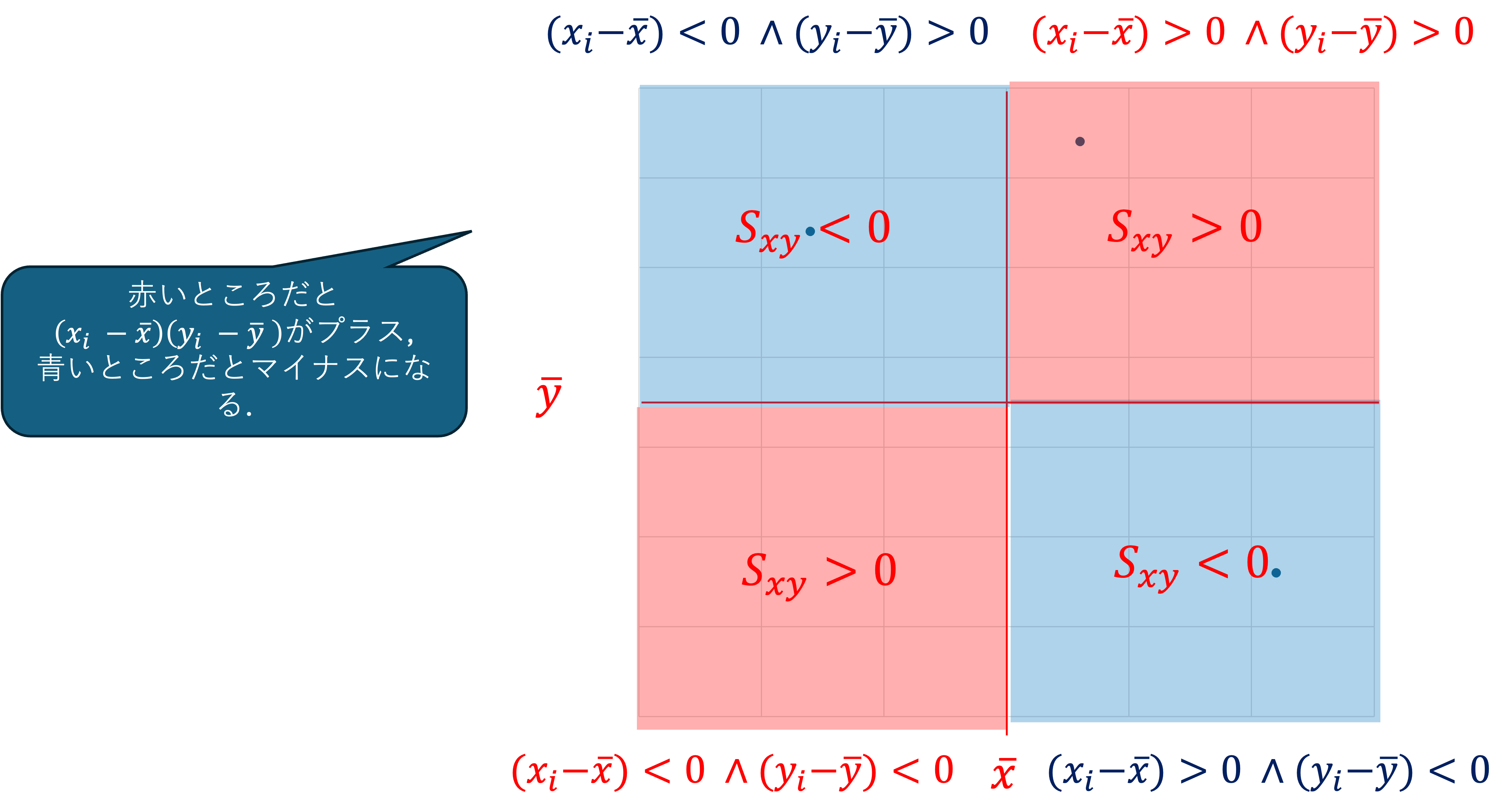
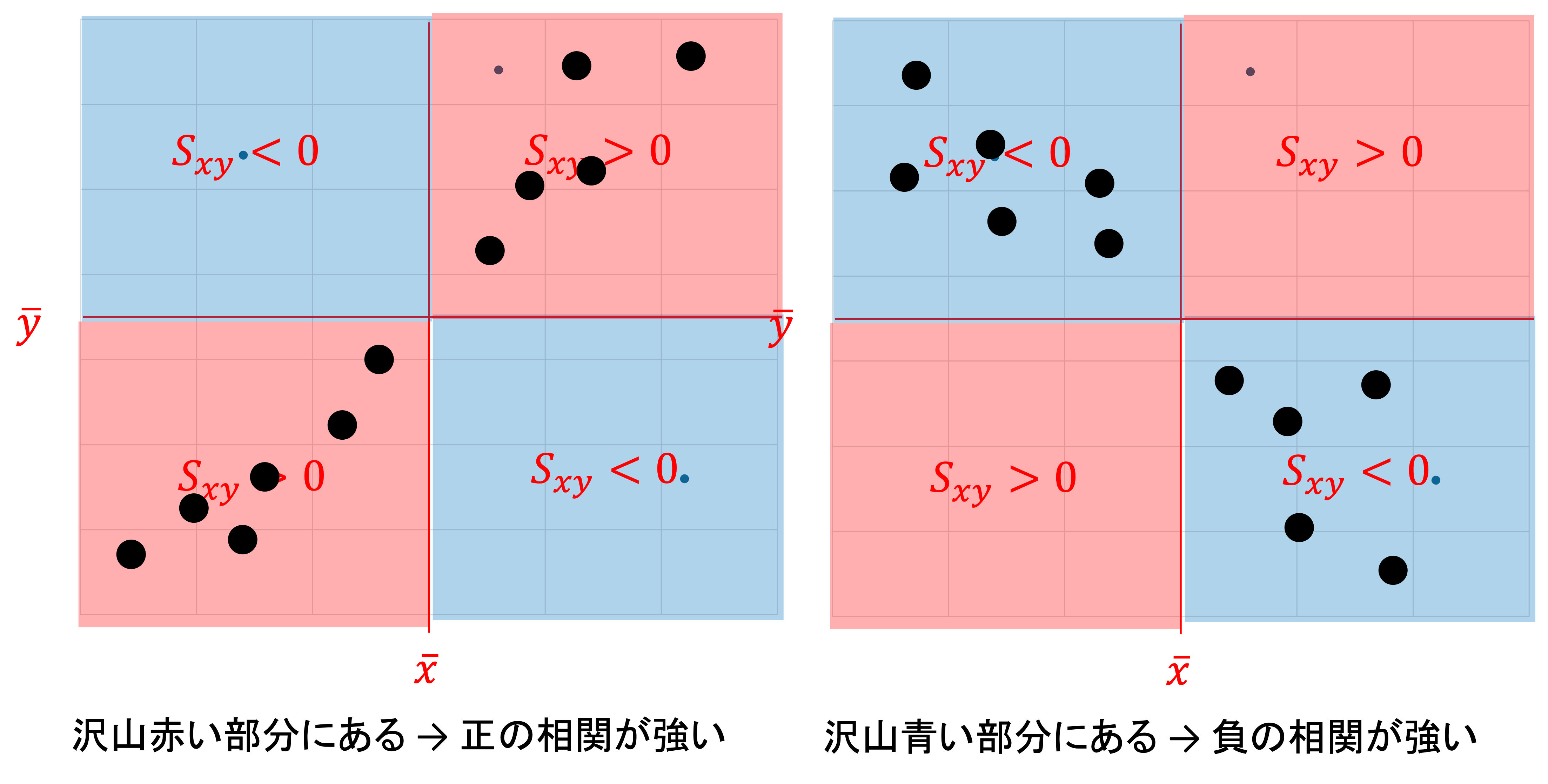
x_i, y_i を標準化し z_i = \frac{x_i - \bar{x}}{s_x}, w_i = \frac{y_i - \bar{y}}{s_y} とすると,
\begin{align*} r_{zw} &= \frac{1}{n} \sum z_i w_i \\ &= \frac{1}{n S_z S_w} \sum (x_i - \bar{x})(y_i - \bar{y}) \\ &= \frac{1}{n} \sum \left( \frac{x_i - \bar{x}}{S_x} \right) \left( \frac{y_i - \bar{y}}{S_y} \right) \\ &= \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{n S_x S_y} \\ &= r_{xy} \end{align*}
このとき,証明の為に \frac{1}{n} \sum (z_i \pm w_i)^2 を考える.
\begin{align*} \frac{1}{n} \sum (z_i \pm w_i)^2 &\geq 0 \\ \frac{1}{n} \sum (z_i^2 \pm 2z_i w_i + w_i^2) &\geq 0 \\ \frac{1}{n} \sum z_i^2 \pm \frac{2}{n} \sum z_i w_i + \frac{1}{n} \sum w_i^2 &\geq 0 \\ \frac{1}{n S_x^2} \sum (x_i - \bar{x})^2 \pm \frac{2}{n} \sum z_i w_i + \frac{1}{n S_y^2} \sum (y_i - \bar{y})^2 &\geq 0 \\ \frac{S_x^2}{S_x^2} + \frac{2}{n} \sum z_i w_i + \frac{S_y^2}{S_y^2} &\geq 0 \\ 1 \pm \frac{2}{n} \sum z_i w_i + 1 &\geq 0 \\ 2 (1 \pm r_{xy}) &\geq 0 \\ -1 \leq r_{xy} \leq 1 \end{align*}
このように相関係数は常に -1 \leq r_{xy} \leq 1 を取ります.
また, cをc > 0の定数として$すべての点で x_i = c y_i が成り立つとき, \bar{x} = c \bar{y_i} が成り立ち,
\begin{align*} S_y &= \sqrt{\frac{1}{n} \sum (y_i - \bar{y})^2} \\ &= \sqrt{\frac{1}{n} \sum (c x_i - c \bar{y})^2} \\ &= \sqrt{\frac{c^2}{n} \sum (x_i - \bar{x})} \end{align*}
となります. したがって,
\begin{align*} r &= \frac{\frac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y})}{S_x \times S_y} \\ &= \frac{\frac{c}{n} \sum (x_i - \bar{x})(x_i - \bar{x})}{S_x \times S_x} \\ &= \frac{c S_x^2}{c S_x^2} = 1 \end{align*}
となり,1となります. また, c < 0 の場合は, S_x \times S_y = -c S_x^2となるので,-1になります.
このようにx_iとy_iが同じ比率で増減するとき,
- r_{xy} = 1 となり,正の完全相関
- r_{xy} = -1 となり,負の完全相関
といいます.
なお, 相関が「ある/ない」の目安は以下のようになっています.
| 相関係数 | 関連性の程度 |
|---|---|
| 0.0~0.4 ,0.0~-0.4 | ほとんど相関がない |
| 0.4~0.7 ,-0.4~-0.7 | 弱い相関がある |
| 0.7~0.9 ,-0.7~-0.9 | 強い相関がある |
| 0.9~1.0 ,-0.9~-1.0 | きわめて強い相関がある |
Pythonで積率相関係数を求めるには numpyのnp.corrcoef(xのデータ,yのデータ)あるいは,scipy.stats.pearsonr(xのデータ,yのデータ)を利用します. scipyがインストールされていない人は pip install scipyをしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
import scipy.stats as st
#データの読み込み
#データの位置を指定しよう
df = pd.read_csv('Data/scatter.csv')
print(df)
#散布図のx軸を指定
x_column = 'AI'
#散布図のy軸を指定
y_column = 'Python'
x_value = df[x_column]
y_value = df[y_column]
plt.scatter(x_value, y_value)
plt.ylabel(y_column)
plt.xlabel(x_column)
plt.show()
# numpyで相関係数を求める
# 返り値が [[xとxの相関係数=1, xとyの相関係数]
# ,[yとxの相関係数, yとyの相関係数=1]]
# となっている
print(np.corrcoef(df[x_column],df[y_column]))
"""
[[1. 0.83281294]
[0.83281294 1. ]]
"""
print(np.corrcoef(df[x_column],df[y_column])[0][1])
# 0.83281294
#scipy.stats.pearsonr でも計算可能
# 返り値が (相関係数, p値)の形に成っている
# p値に関しては, 検定の章で扱います.
r, p = st.pearsonr(df[x_column],df[y_column])
print(r) #0.83281293789616211.4.2 スピアマンの順位相関係数
積率相関係数は量的変数にしか利用できませんが,質的変数のうち順序尺度データに関しては,スピアマンの順位相関係数(rank correlation coefficient)が利用できます.
スピアマンの順位相関係数は, 順序尺度データを順位に変換して,順位の間の相関係数を求めたものになります.
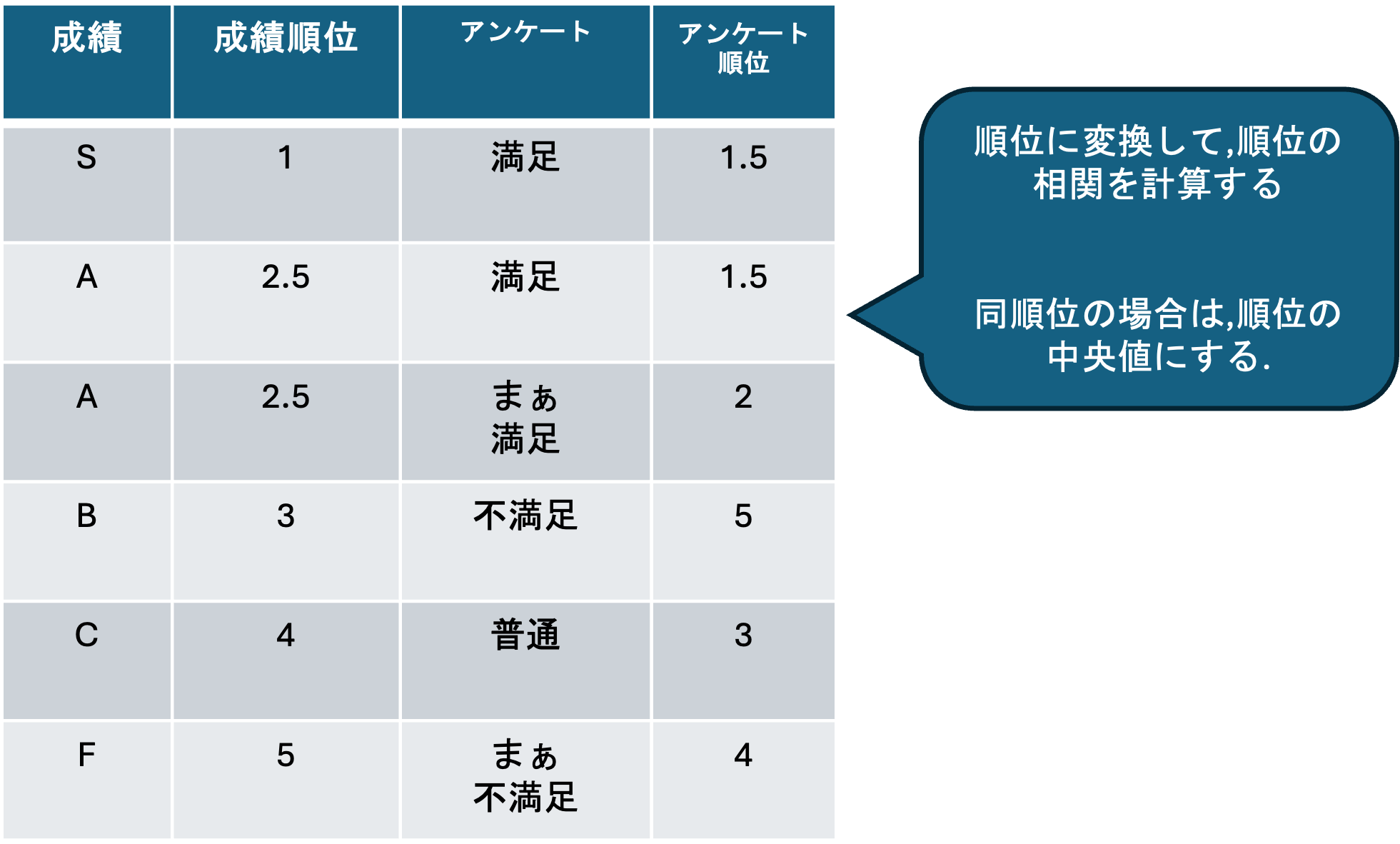
データを小さい順に並べ替えた順位 x_i, ..., x_n がある時,
r_{xy} = \frac{\frac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\frac{1}{n} \sum (x_i - \bar{x})^2} \sqrt{\frac{1}{n} \sum (y_i - \bar{y})^2}} がどの様になるかを考える.
順位相関係数は,
\sum x_i = \sum y_i = \frac{n(n+1)}{2}
\sum x_i^2 = \sum y_i^2 = \frac{1}{6} n(n+1)(2n+1)
\bar{x} = \bar{y} = \frac{\sum x_i}{n} = \frac{n(n+1)}{2n} = \frac{n+1}{2}
なので, 分子に関して,
\begin{align*} & \frac{1}{n}\sum(x_i - \bar{x})(y_i - \bar{y}) \\ &= \frac{1}{n}\sum \{x_iy_i - x_i \bar{y} - \bar{x}y_i + \bar{x}\bar{y}\} \\ &= \frac{1}{n}\sum x_i y_i - \frac{1}{n}\sum x_i\bar{y} - \frac{1}{n}\sum \bar{x}y_i + \frac{1}{n}\sum \bar{x}\bar{y} \\ &= \frac{1}{n}\sum x_i y_i - \frac{\bar{y}}{n}\sum x_i - \frac{\bar{x}}{n}\sum y_i + \bar{x}\bar{y} \\ &= \frac{1}{n}\sum x_i y_i - \bar{x}\bar{y} \\ &= \frac{1}{2n}\sum \{x_i^2 + y_i^2 - (x_i - y_i)^2\} - \bar{x}\bar{y} \\ \end{align*}
\begin{align*} \because (x_i - y_i)^2 = x_i^2 -2x_i y_i + y_i^2 \\ x_i y_i = \frac{1}{2} \{ x_i^2 + y_i^2 - (x_i - y_i)^2 \} \end{align*}
\begin{align*} & \frac{1}{2n}\sum \{x_i^2 + y_i^2 - (x_i - y_i)^2\} - \bar{x}\bar{y} \\ &= \frac{1}{2n}\sum x_i^2 + \frac{1}{2n}\sum y_i^2 - \frac{1}{2n}\sum (x_i - y_i)^2 - \bar{x}\bar{y} \\ & = \frac{1}{6} (n+1)(2n+1) - \frac{(n+1)^2}{4} - \frac{1}{2n}\sum (x_i - y_i)^2 \\ & = \frac{1}{12}(n+1)(n-1) - \frac{1}{2n}\sum (x_i - y_i)^2 \end{align*}
また, 分母に関して, \begin{align*} & \frac{1}{n}\sum (x_i - \bar{x})^2 \\ &= \frac{1}{n}\sum x_i^2 - n \bar{x}^2 \\ &= \frac{1}{n} \{ \sum x_i^2 -2n \bar{x}^2 + \bar{x}^2 \} \\ &= \frac{1}{n} \{\sum x_i^2 - n\bar{x}^2\} \\ &= \frac{1}{6}(n+1)(2n+1) - \frac{1}{4}(n+1)^2 \\ &= \frac{1}{12}(n+1)(n-1) \end{align*}
なので
r_{xy} = \frac{\frac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\frac{1}{n} \sum (x_i - \bar{x})^2} \sqrt{\frac{1}{n} \sum (y_i - \bar{y})^2}}
に代入して, \begin{align*} r_{xy} = \frac{\frac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\frac{1}{n} \sum (x_i - \bar{x})^2} \sqrt{\frac{1}{n} \sum (y_i - \bar{y})^2}} &= \frac{\frac{1}{12}(n+1)(n-1) - \frac{1}{2} \sum (x_i - y_i)^2}{\frac{1}{12}(n+1)(n-1)}\\ &= 1 - \frac{6}{n^3 - n} \sum (x_i - y_i)^2 \end{align*}
となる.
スピアマンの順位相関係数は,Pythonでは, scipy.stats.spearmanr(xのデータ,yのデータ)で求めることができます.
こちらのデータは,国別(A~J)のサッカー(FIFA)と野球(WBSC)のランキングのダミーデータです.
rank FIFA WBSC
0 1 A A
1 2 B E
2 3 C G
3 4 D I
4 5 E D
5 6 F C
6 7 G B
7 8 H F
8 9 I H
9 10 J Jこちらの順位の相関係数を求めてみましょう.
df = pd.read_csv('Data/spearman.csv')
# sciypyで相関係数を求める
correlation, pvalue = st.spearmanr(df["FIFA"], df["WBSC"])
print("相関係数:",correlation) #0.45450.45なので弱い正の相関があることが分かります.
1.4.3 相関係数のヒートマップ
相関係数はデータの関係を探るために非常に便利な数値であり, 複数の観測項目からなるデータを扱う場合には,最初に相関係数をとってそれぞれにどのような関係があるのかを確認するようにしましょう.
こちらのデータは,e-statから取得した,県別の身長,体重,食費,睡眠の平均時間,スポーツの平均時間に関するデータです.
python coeff.py
pref height weight food sleep sports
0 北海道 170.4 63.7 65739 477 15
1 青森県 169.8 62.8 64889 490 13
2 岩手県 170.6 63.7 70156 489 13
3 宮城県 169.8 63.4 73337 482 15
4 秋田県 170.6 66.1 74560 493 14
5 山形県 170.9 63.9 76000 497 12
6 福島県 170.2 63.9 71074 480 13
7 茨城県 169.7 62.4 74341 467 17
8 栃木県 169.8 63.3 74387 472 16
9 群馬県 170.5 62.7 71701 475 15
10 埼玉県 170.4 61.1 76663 463 15
11 千葉県 170.3 62.4 77639 458 15
12 東京都 170.5 61.3 83506 461 16
13 神奈川県 170.9 62.5 77510 456 17
14 新潟県 170.9 62.0 75937 479 13
15 富山県 170.8 63.5 73589 471 15
16 石川県 170.8 62.9 76256 470 16
17 福井県 170.4 62.5 79478 476 14
18 山梨県 170.1 61.7 71294 481 16
19 長野県 169.5 61.0 72228 474 17
20 岐阜県 169.9 60.6 69527 469 13
21 静岡県 170.1 61.9 75833 474 19
22 愛知県 169.6 60.9 74694 463 14
23 三重県 170.4 62.1 75721 473 16
24 滋賀県 170.6 62.9 77978 470 18
25 京都府 170.5 62.0 76904 464 16
26 大阪府 170.2 62.2 74015 469 18
27 兵庫県 169.6 60.6 72847 466 15
28 奈良県 169.9 61.8 74888 461 18
29 和歌山県 170.0 62.6 69858 479 15
30 鳥取県 170.4 62.7 73321 475 14
31 島根県 169.7 60.7 72160 483 16
32 岡山県 169.6 61.7 69060 475 17
33 広島県 168.8 60.8 69061 473 15
34 山口県 169.2 60.2 69882 472 17
35 徳島県 169.9 64.4 67102 472 18
36 香川県 169.9 62.7 68400 469 18
37 愛媛県 168.8 61.8 67274 474 16
38 高知県 169.1 61.8 70188 484 16
39 福岡県 169.7 60.9 70135 471 14
40 佐賀県 169.2 62.2 68749 473 16
41 長崎県 170.1 63.3 66641 473 18
42 熊本県 169.5 61.8 66184 482 20
43 大分県 169.3 62.5 69255 479 18
44 宮崎県 168.7 61.8 65165 477 19
45 鹿児島県 169.7 61.4 65377 479 18
46 沖縄県 168.7 60.6 56298 482 20データの取得過程に興味がある人は,以下の手順を自分で行い,データを作ってみましょう.
e-statのデータ表示機能を使ってデータを自分で作る (開く/閉じる)
e-statで県別の身長,体重,睡眠時間等のデータを集めます. 地域別のデータは「地域」から選択できます.
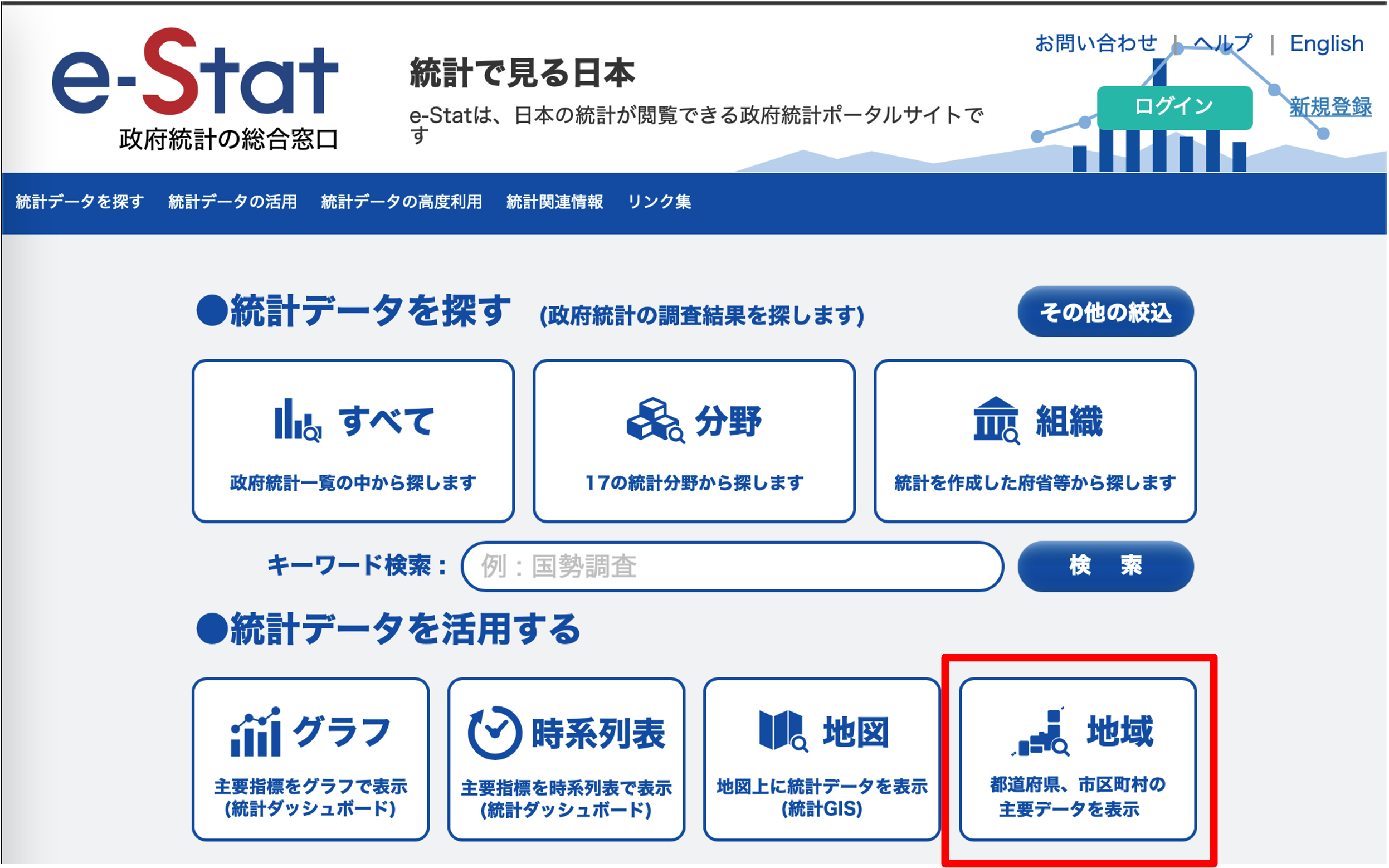
「都道府県データ」を選択し,「データ表示」をクリックします.
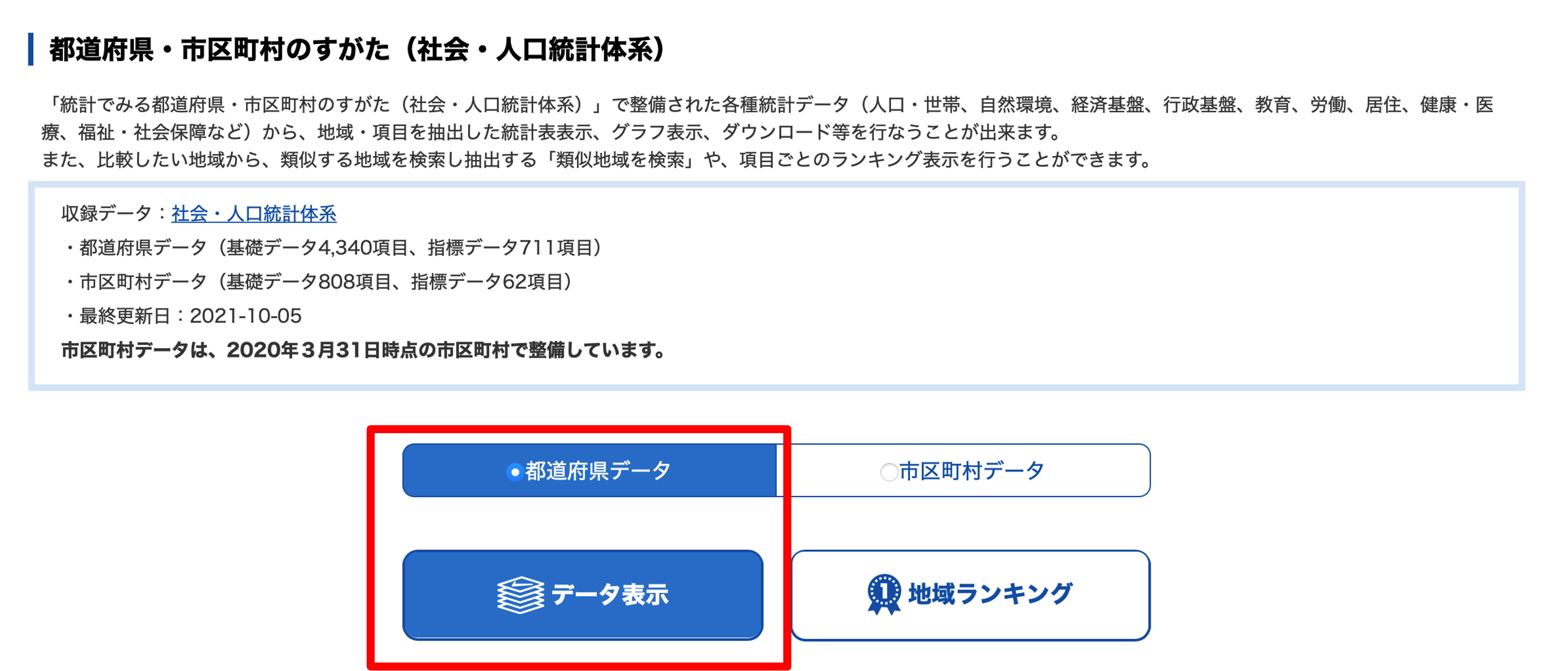
データを集める,地域,表示項目,表示方法の順に選択します. 今回はすべての県を利用するので,「全て選択」をクリックしたあと「確定」をクリックします.
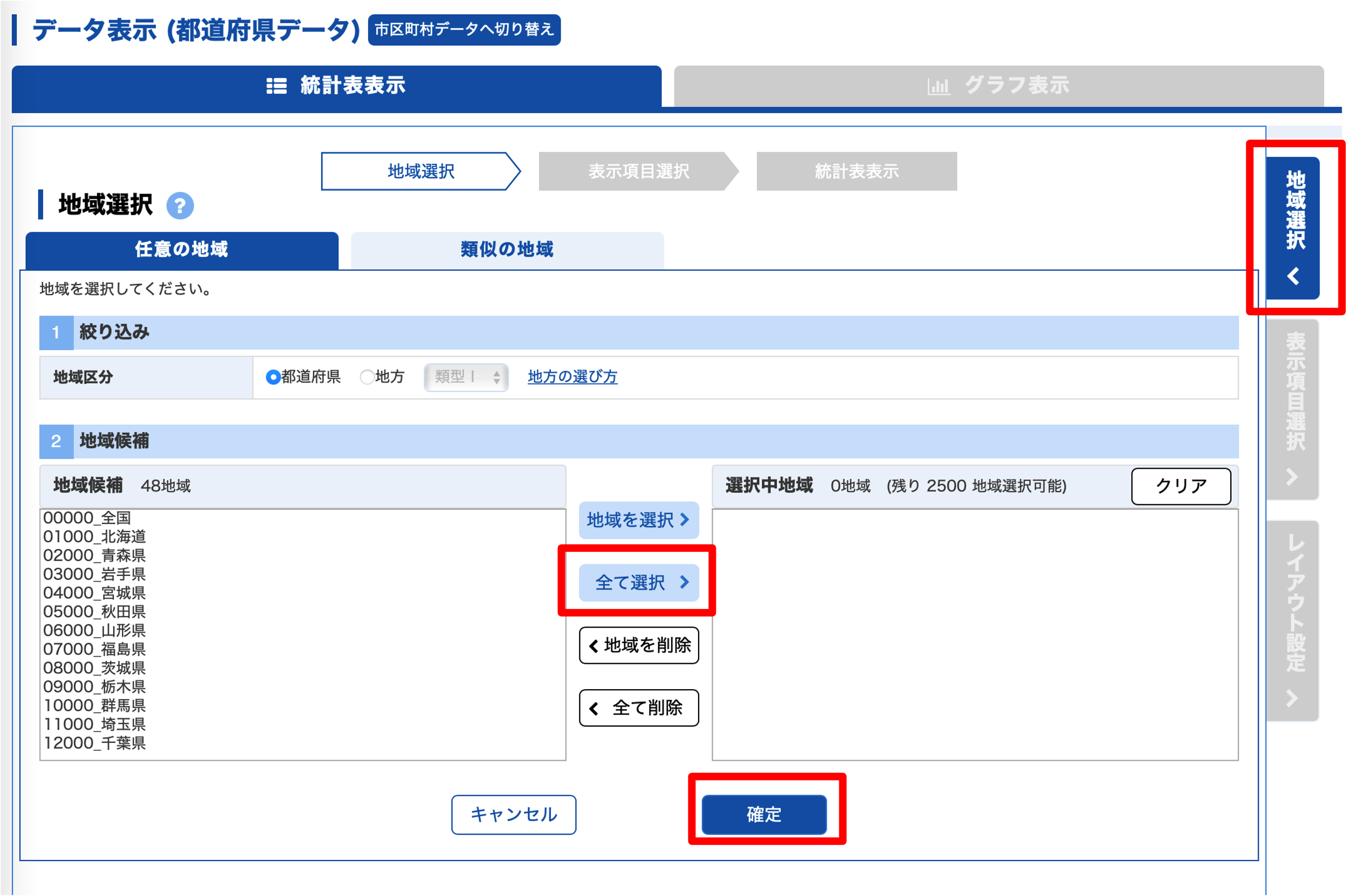
次に項目をきめます. 分野をクリックして「I健康・医療」を選ぶと,項目候補に健康・医療に関わる項目が表示されます. そこから,
- I411301_身長(高校2年)(男)【cm】
- I412301_体重(高校2年)(男)【kg】を順番に選んで,「項目を選択」をクリックします.
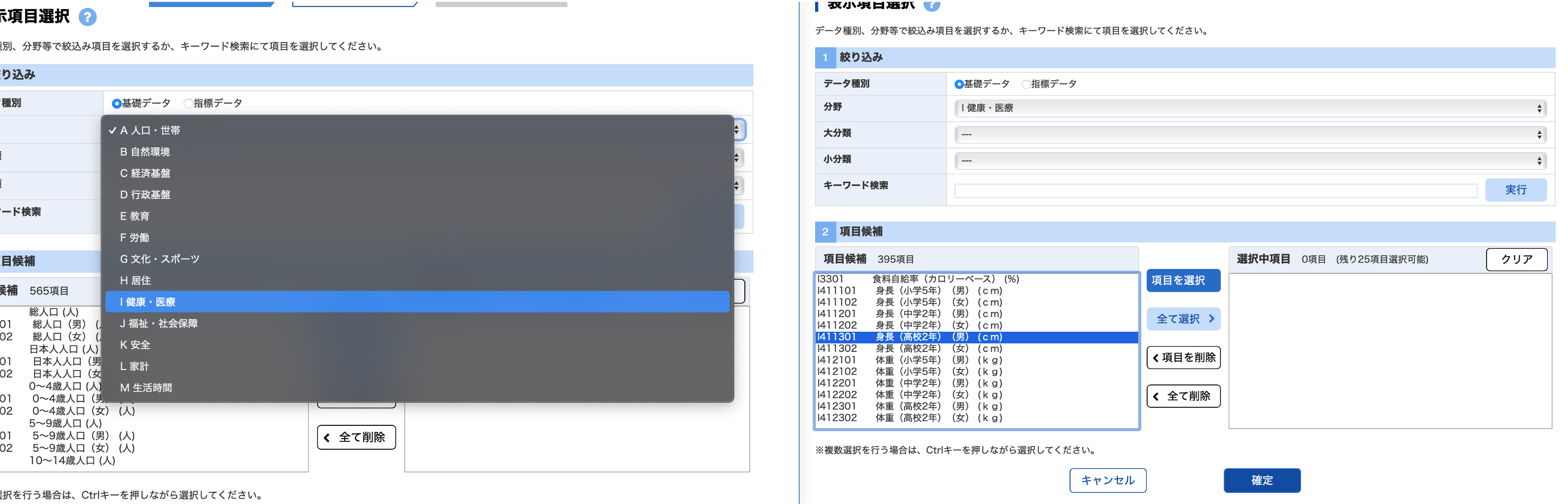
同様に 「L 家計」から
- L421101_食料費(二人以上の世帯のうち勤労者世帯)(全国消費実態調査結果)【円】「M 生活時間」から
- M1101_睡眠の平均時間(10歳以上)(男)【分】
- M360100_スポーツの平均時間(15歳以上)(男)【分】を順番に選んで,「項目を選択」をクリックします.
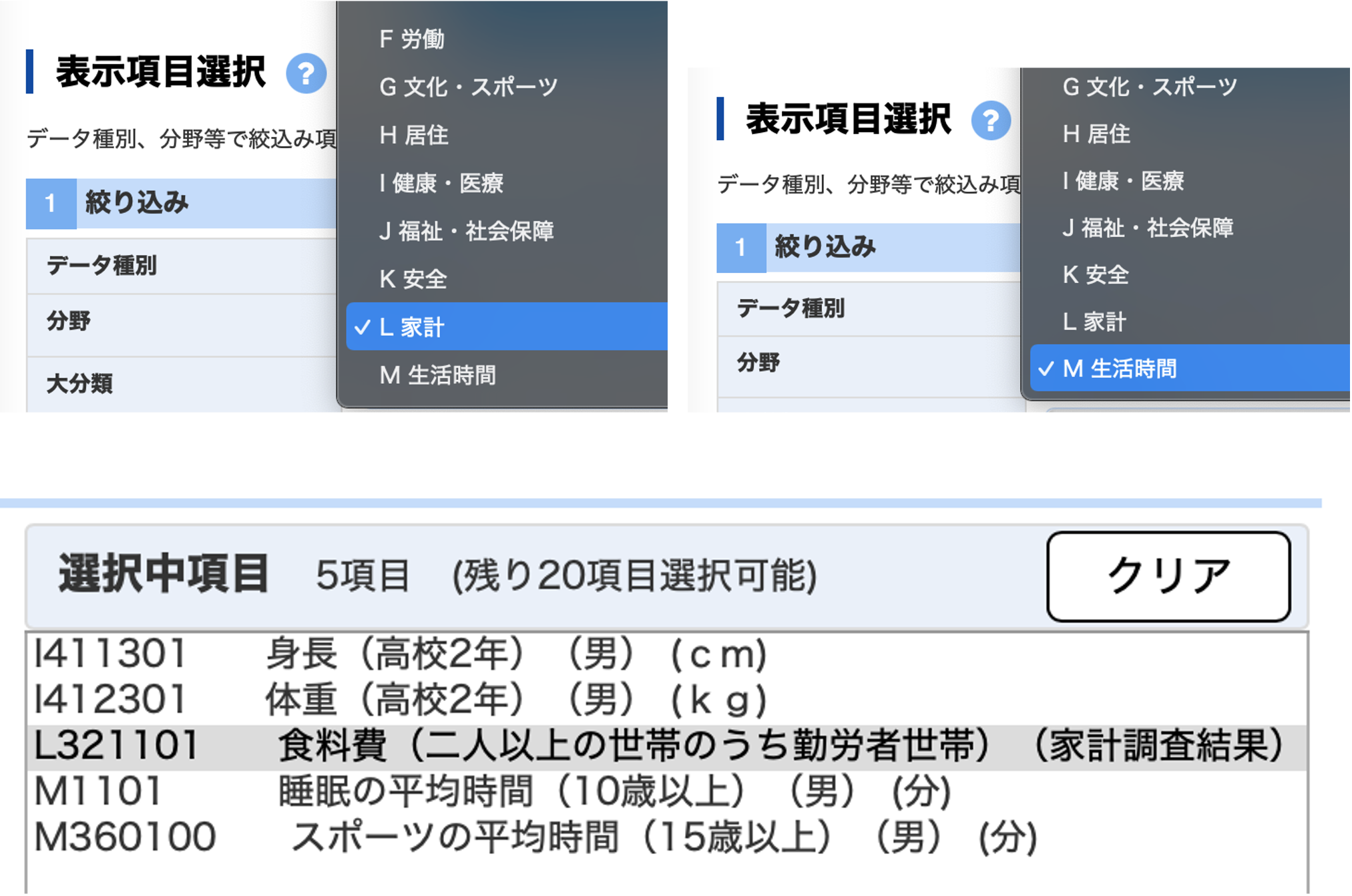
最後にどのデータを表示するかレイアウトを決めます.
- 調査年を列に配置
- 表示年度を2000から2010まで
- 設定して表示を更新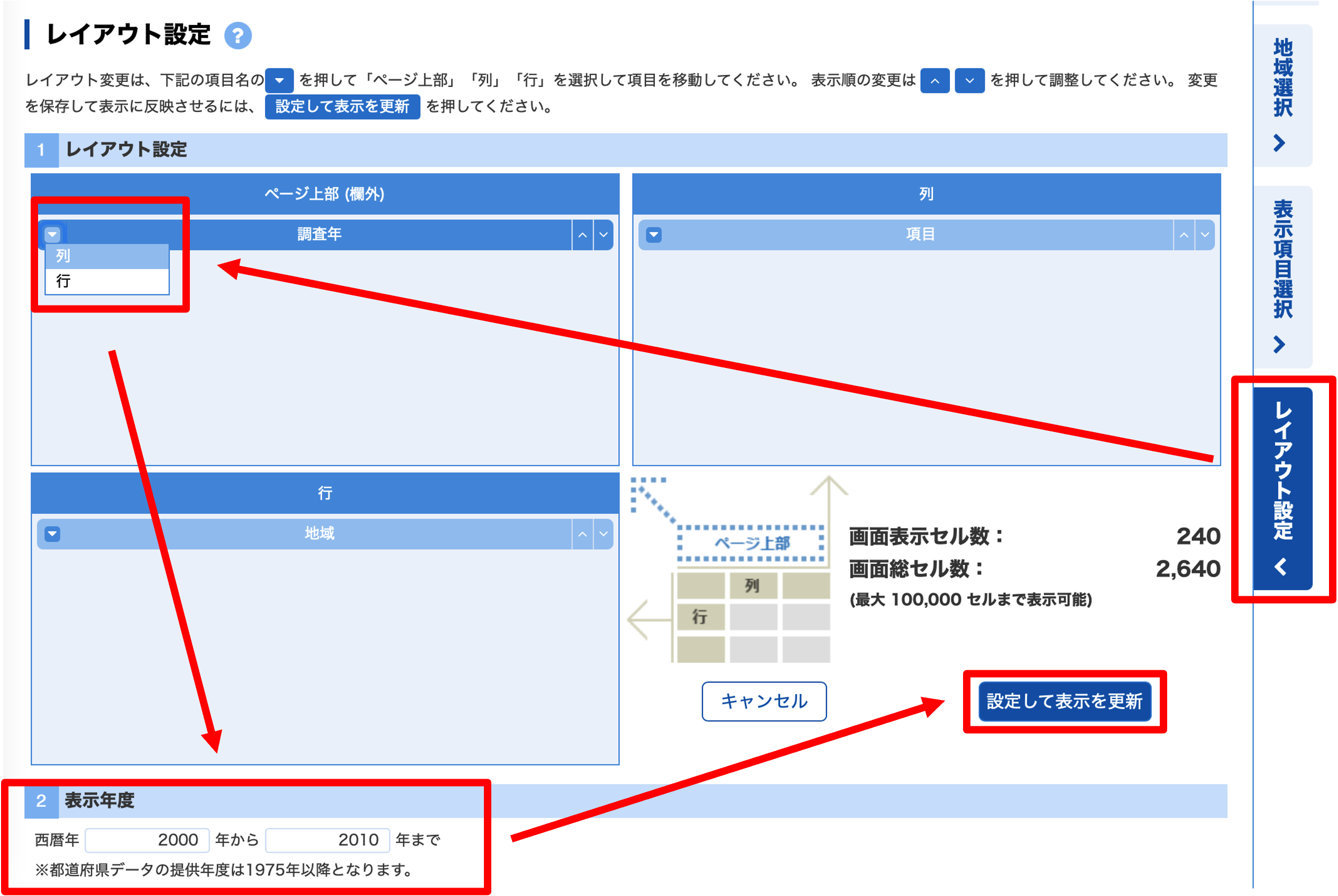
データをダウンロードします.
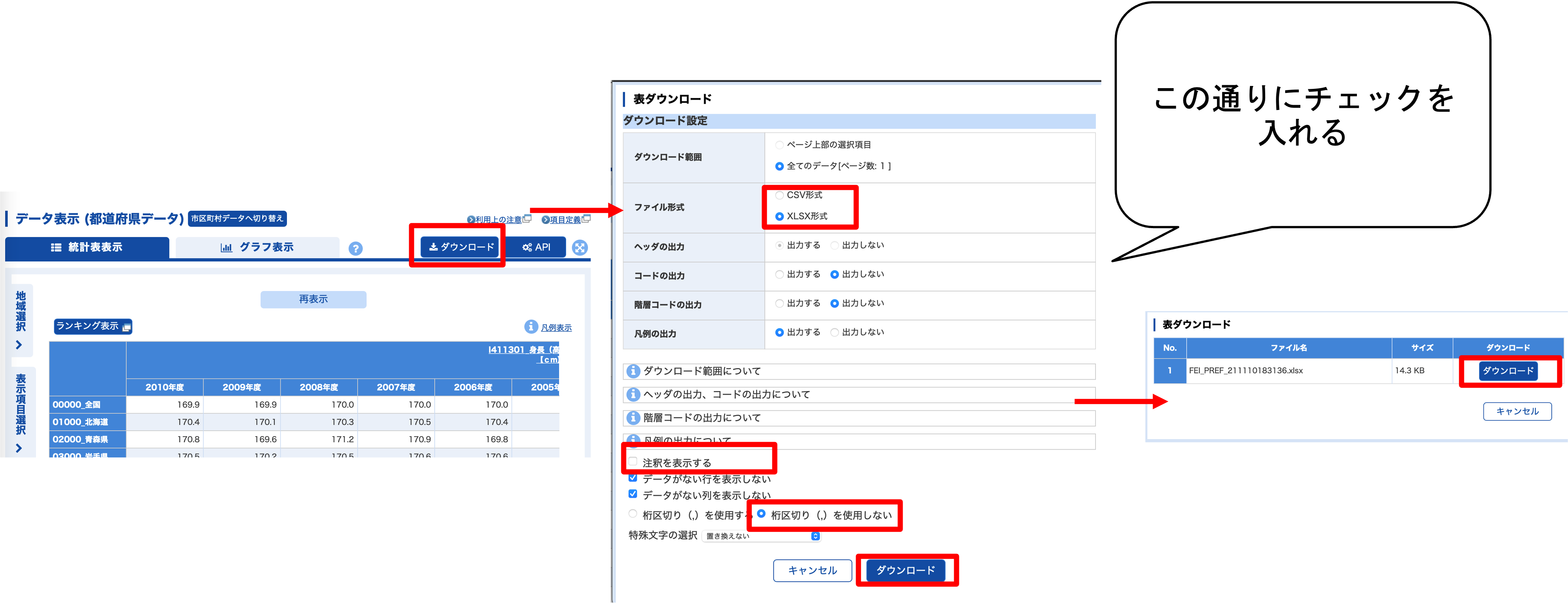
ダウンロードしたデータを読み込めるcsvに編集します.
- 2006年以外の列を削除
- 数値として新しいシートにコピー
- ヘッダー名をつける
- 県名 pref (prefectureの略)
- 身長 height
- 体重 weight
- 食費 food
- 睡眠 sleep
- スポーツ sports
- utf-8のcsvで保存
- ファイル名: coeff_multi.csv
- 作業ディレクトリのDataフォルダに保存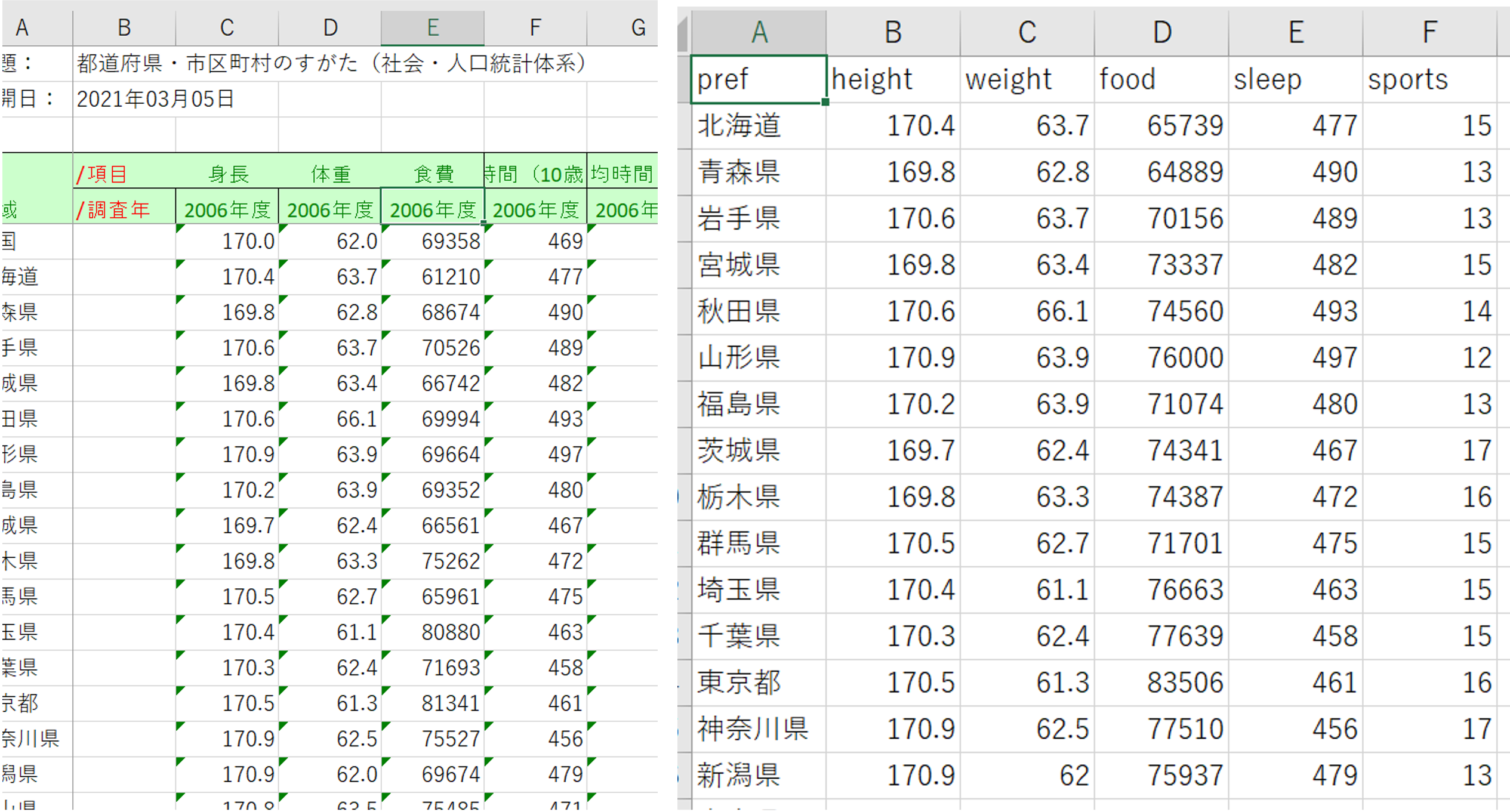
データのどの観測項目間に関連があるのかを確かめるために,作成したデータのすべての組み合わせの相関係数を見てみましょう. 今までのように一つ一つ散布図を作成して,相関係数を求めていると,\text{観測項目数} \times \text{観測項目数} のグラフを作成することになります. そこで, 与えられた観測項目すべての組み合わせで図示するペアプロットとヒートマップを活用してみます.
DataFrameに含まれるデータのペアプロットには, pandasの.plottingメソッドを利用します. pd.plotting.scatter_matrix(ペアプロットを求めるDataFrame)で,散布図のペアプロットが作成できます.
また, 各項目の相関係数もpandasの.corr()メソッドで取得することが出来ます.
# CSVファイルを読み込んでデータフレームに格納
# Dataフォルダを作成し,そこにデータを入れておきましょう
df = pd.read_csv('Data/coeff.csv')
# データの表示
print(df)
#分析するデータの選択
labels = ['height', 'weight', 'food', 'sports', 'sleep']
X = df[labels]
#散布図行列を作成してみる
pd.plotting.scatter_matrix(X, range_padding=0.2)
plt.show()
#相関係数の組み合わせを確認
print(X.corr())
#ヒートマップで確認
#ヒートマップで確認
sns.heatmap(X.corr()
,vmax=1 #ヒートマップの最大値
,vmin=-1 #最小値
,center =0 #中心
,annot=True)
plt.show()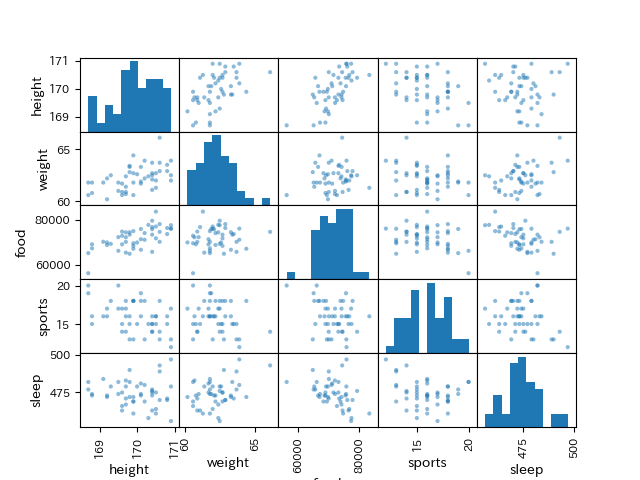 各項目の組み合わせごとに,散布図が作成されています. 自交点にはヒストグラムが作成されます.
各項目の組み合わせごとに,散布図が作成されています. 自交点にはヒストグラムが作成されます.
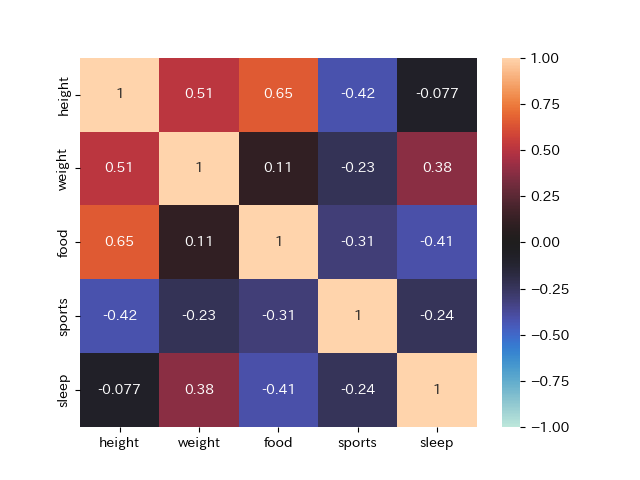
食費と体重,体重と身長などに正の相関があることが分かります. このように複数の観測項目から関係があるデータを探したい場合には,ペアプロットや,相関係数のヒートマップを作成することで,関係性がわかりやすくなります.
1.4.4 \Chi^2統計量
量的データには積率相関係数, 順位尺度データに対しては,順位相関係数を求めることで2つのデータの関連性を確かめることができました. では,名義尺度データの場合はどのようにすれば良いのでしょうか.
名義尺度を含めた質的変数の関係性を可視化するには,同時度数分布表が利用できました. 数値化においても,同時度数分布表を用いることができます.
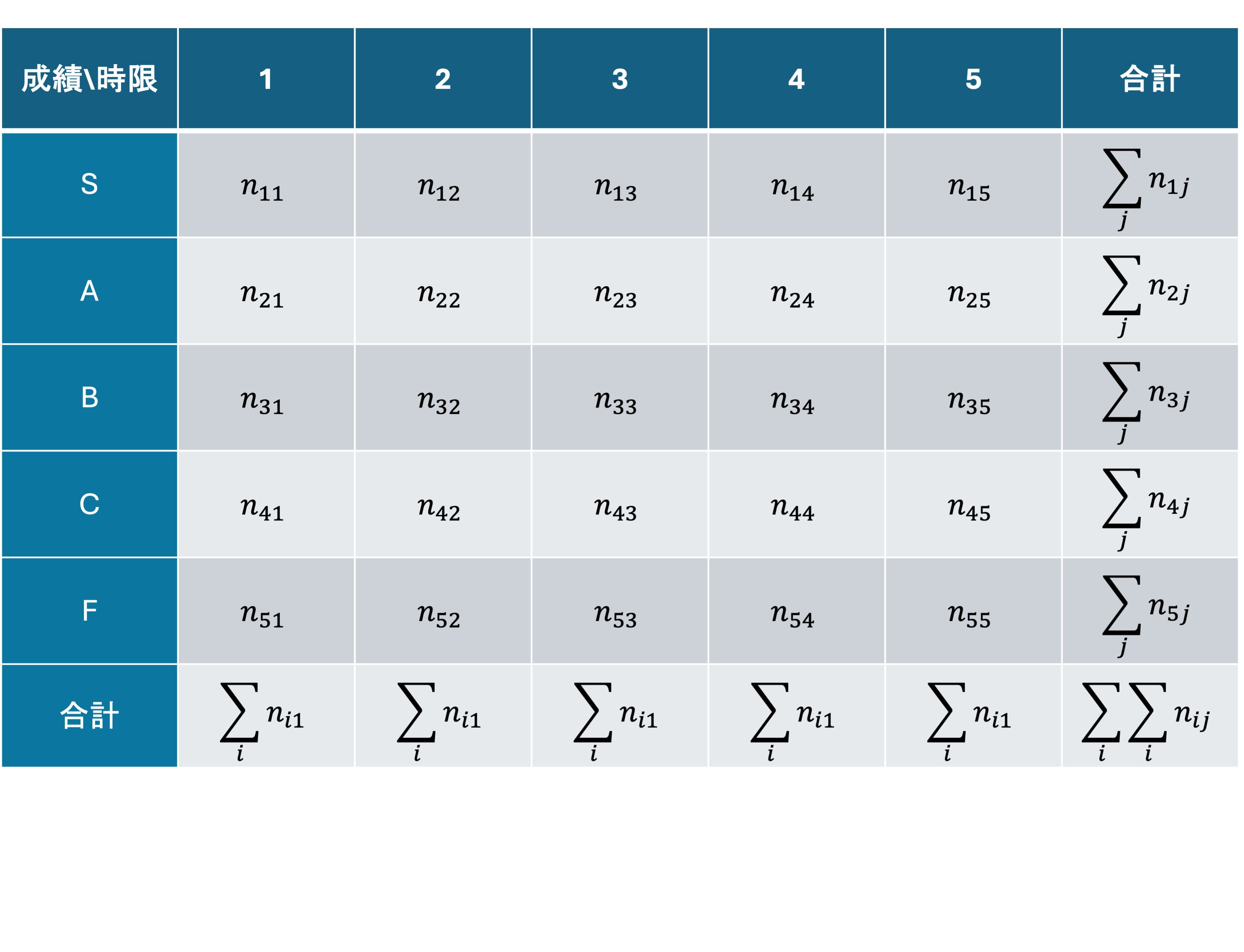
質的変数間の関連度合いは,同時度数分布表の数値を利用した ピアソンの\Chi^2統計量(かいじじょうとうけいりょう)で表すことができます. 可視化の節では, 同時度数分布表から列相対度数を求めましたが,ここでは相対度数ではなく,度数なので注意してください.
\Chi_o^2 = \sum_{i=0}^{r} \sum_{j=0}^{c} \frac{(n_{ij} - E_ij)^2}{E_{ij}} (r:行数,c:列数)
このとき,E_{ij}を期待度数といい, \frac{行の合計 \times 列の合計}{総数}
E_{ij} = \frac{\sum_{i}^r n_{ij} \times \sum_{j}^c n_{ij}}{\sum_{i}^{r}\sum_{j}^c n_{ij}}
で求められます.
この\Chi_o^2が大きいほど,2つの変数の間の関連が強いと言え,この値を利用して行と列のデータが独立であるかを検定する \Chi^2検定(独立性の検定) を行うことができます. ** \Chi^2 検定** に関しては後ほど扱うとして,ここではこの値を利用して2つのデータの関連の度合いを判断する方法に関して見ていきましょう.
\Chi_o^2の値は, 同時度数分布表の行数や列数に依存して値が変わるため,相関係数のように,「特定の値から関連があるといえる」といった利用方には適しません.
そこで, 異なるデータを比較するためには, 0 \leq V \leq 1の値を取る,クラメールの連関係数Vに変換します.
V = \sqrt{\frac{\Chi_o^2}{n \times min(r - 1,c - 1)}}
クラメールの連関係数は,相関係数よりも高い値が出にくいので,以下のような基準で判断します.
| V | 判断 |
|---|---|
| 0 ~ 0.1 | 関連なし |
| 0.1 ~ 0.25 | 弱い関連がある |
| 0.25 ~ 0.5 | 関連がある |
| 0.5 ~ 1.0 | 強い関連がある |
\Chi_o^2は scipy.statsのchi2_contingency(度数分布表,correction=False)で求めることが出来ます.
返り値が, \Chi_o^2,p値,自由度,期待度数の4つあるので,注意しましょう.
同時度数分布表の節で扱った時限と成績の関係を記録したデータを利用して,クラメールの連関係数Vを求めてみましょう.
Period Grade
0 2 B
1 5 A
2 4 A
3 3 C
4 1 C
.. ... ...
195 2 C
196 4 C
197 5 C
198 5 F
199 4 C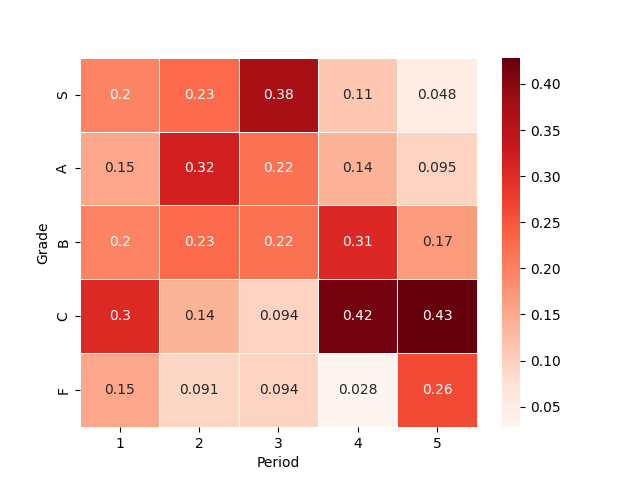
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as st
import numpy as np
df = pd.read_csv('data/cross_table_data.csv')
#クロス表の作成
cross = pd.crosstab(df['Grade'],df['Period'])
#表示順の設定
cross = cross.reindex([1,2,3,4,5],axis='columns')
cross = cross.reindex(['S','A','B','C','F'],axis='index')
print(cross)
#列相対度数に変更する
for c in cross.columns:
cross[c] = cross[c] / cross[c].sum()
print(cross)
sns.heatmap( cross #ヒートマップを作成したいテーブル
, cmap=plt.get_cmap('Reds') #カラーマップ(省略可)
, linewidths=.5 #線の太さを指定することでセルを囲う線を表示
, annot=True #セルに数値を表示
)
plt.show()
#χ二乗統計量を求める
x2, p, dof, e = st.chi2_contingency(cross,correction=True)
print(x2) #1.1342960955202308
#クラメールの連関係数Vを求める
v = np.sqrt(x2/(cross.sum().sum() * min(cross.shape[0]-1,cross.shape[1] -1)))
print(v) #0.2381487030743849クラメールの連関係数Vの値は,0.28となり,弱い関連があることが分かりました.
1.4.5 因果関係と相関
相関関係は, 2つの観測項目間の関係を表していますが, 観測項目Aの変化によって,観測項目Bの変化が起きているという因果関係(causality)を示しているものではありません.
論理学における因果関係は, AならばB (A \Rightarrow B) という関係として示されます.
- 例: 人間ならば死ぬこのとき,Aを十分条件, Bを必要条件 といいます.
しかし,統計学における因果関係は,このような関係では表せません. 例えば, 喫煙をすると肺がんになるという関係は, 喫煙をしても肺がんにならない場合があるので,倫理学における因果関係ではありません. 統計学における因果関係は, Aが,Bの一部を説明するための,あるいはBが起きる確率を高めるための十分条件となっていることを表します.
したがって,統計学における因果関係は, ** AによってBの一部が説明できる** あるいは, ** AによってBが起きる確率が高まる** という形で示され,これを統計的因果関係といいます.
統計的因果関係が認められる条件は,簡単には以下のように示されます.
AとBの間に明瞭な関係が認められる
Aが時間的に,あるいは意味的にBより選考している
AとBの共通要因となりうる要因を統制して(影響を取り除いて)も,両者に関係が見出される.
これらの因果関係を示すには, 特に3.に関して, A以外の条件を揃えてBの発生確率を確かめる対照実験などの手法によって明らかにされますが,本資料では実験に関しては扱いません. AによってBを説明する,という関係に関しては,後の回帰の章で少し扱います.
このように, 相関関係と因果関係は異なる概念として理解する必要があります.
例えば, 因果関係があっても相関関係がない有名な例として, チーズの消費量と,ベッドシーツに絡まって死ぬ人の数や,プールで溺れた人の数と,ニコラス・ケイジの映画出演数などがあります(こちらのサイト(https://www.tylervigen.com/spurious-correlations)にこういった例が沢山まとめられているので興味のある人は見てみましょう.)
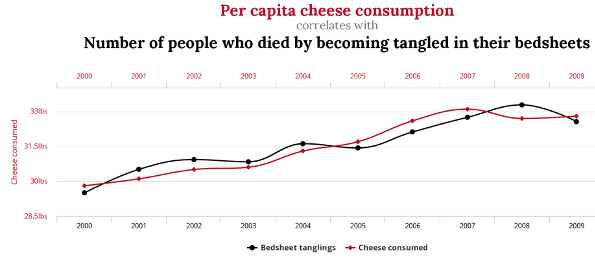
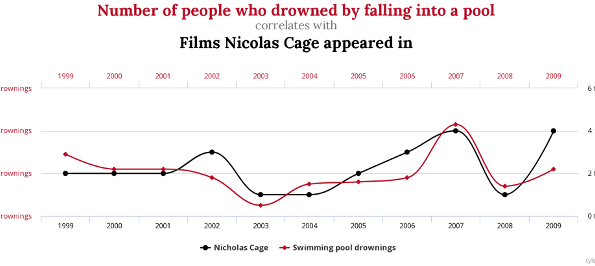
このように,全く因果関係のないものでも現れる相関関係を偽相関(Spurious Correlation)といいます.
また,反対に$ y = (x-8)^2 $ という関係においては, yの値は完全にxによって決まるため,xとyの間に因果関係は認められますが,相関係数は0となります.
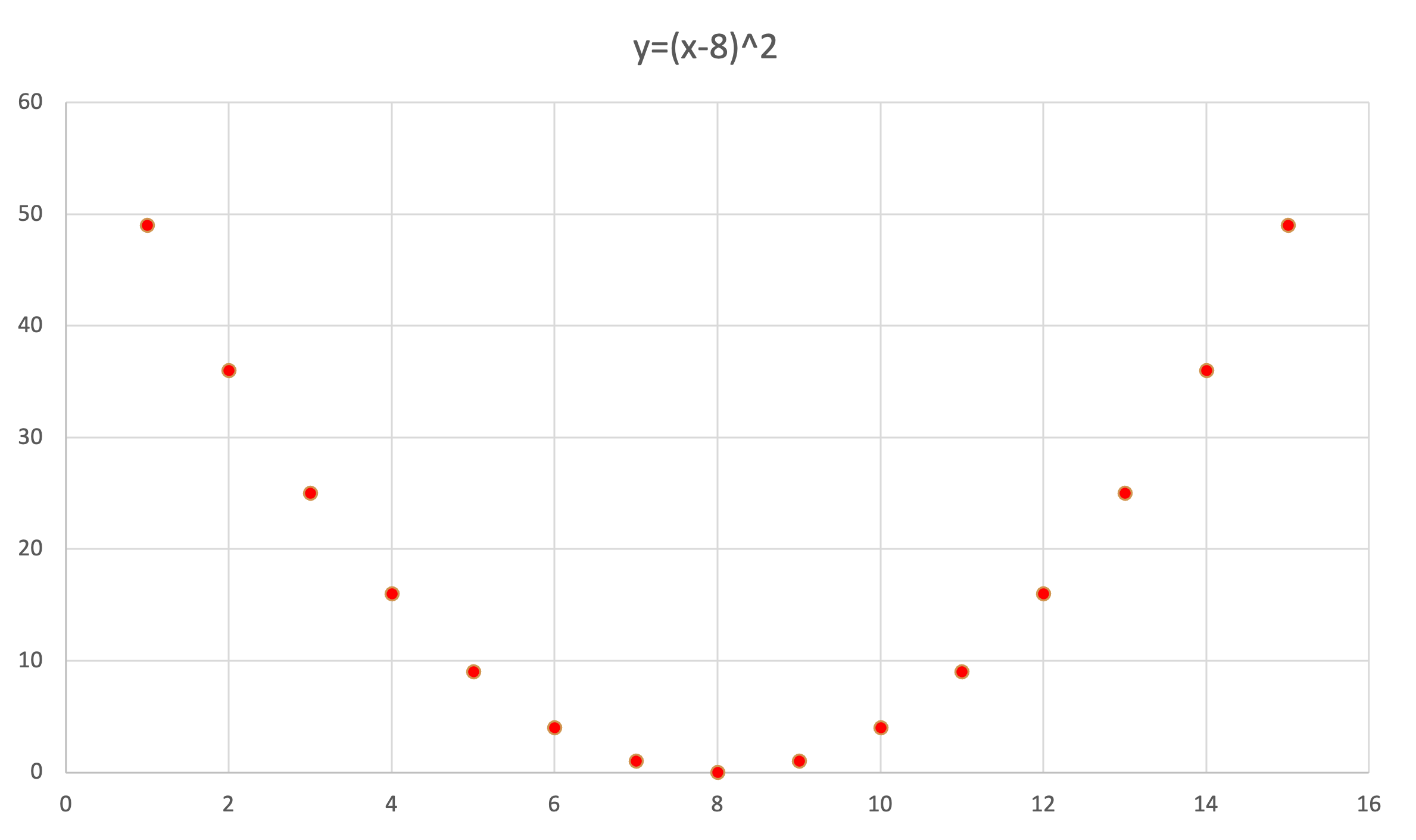
1.4.6 発展:偏相関係数
因果関係を検証する方法に関しては後の章に譲るとして, ここでは,相関における類似概念である偏相関について見てみましょう.
偏相関係数(partial correlation coefficient) とは, 3つの変数がある場合に, 1つの変数の影響を除いた残り2つの変数間の相関係数となります.
変数,x,y,zがあるとき,zの影響を除いた, x,yの間の偏相関係数は以下のように求められます.
r_{xy \dot z} = \frac{r_{xy} - r_{xz}r_yz}{\sqrt{1 - r_{xz}^2}\sqrt{1 - r_{yz}^2}}
式を見てみると,分子では, xとyの相関係数から,zに関する相関係数を引いていることが分かります.
偏相関係数の具体例を見てみましょう. こちらのデータは米国におけるx:小麦の1日あたりの消費量,y:米の一日あたりの消費量,z:肥満度を表しています.なお, いずれの列も最大を1,最小を0に変換してあります.
この3変数の相関係数を取ってみます.
df = pd.read_csv('data/partial_coeff.csv')
x = df['x']
y = df['y']
z = df['z']
#散布図行列を作成してみる
pd.plotting.scatter_matrix(df, range_padding=0.2)
plt.savefig('partial_coeff_scatter_matrix.png')
plt.close()
#ヒートマップで確認
sns.heatmap(df.corr()
,vmax=1 #ヒートマップの最大値
,vmin=-1 #最小値
,center =0 #中心
,annot=True)
plt.savefig('partial_coeff_heatmap.png')
plt.close()
rxy = np.corrcoef(x, y)[0, 1]
rxz = np.corrcoef(x,z)[0, 1]
ryz = np.corrcoef(y,z)[0, 1]
print('x-y:',rxy) #x-y: -0.6001681728315631
print('x-z:',rxz) #x-z: 0.8000777549807391
print('y-z:',ryz) #y-z: -0.4740072261555343
print('ryzx:',ryzx)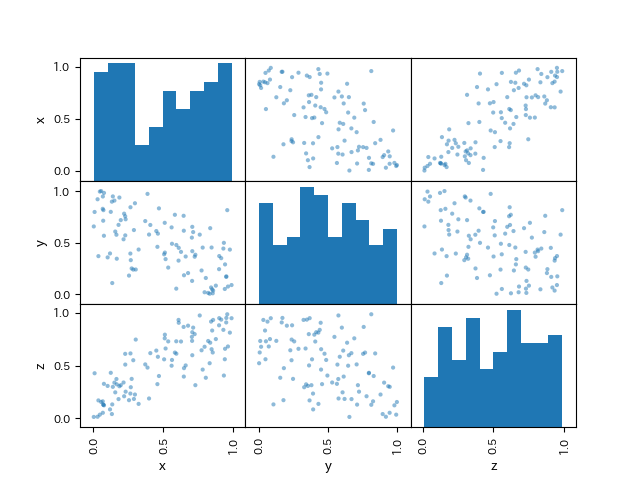
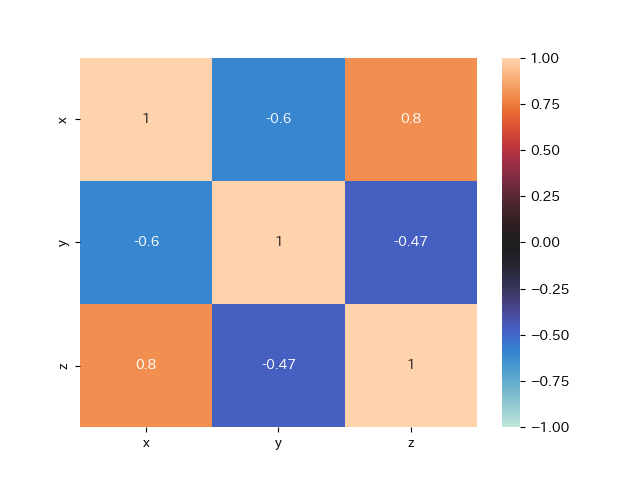
相関係数を見ると,
r_{xy}\approx-0.60: 小麦を食べる量が多いと米を食べる量が少ない
r_{xz}\approx0.80:小麦を食べる量が多いほど太っている
r_{yz}\approx-0.47:米を食べる量が多いほど痩せている
となっています.
小麦を食べるほど,米を食べる量が少ないというのは米国において,米を主食とする人が少ないことから,普段小麦粉を利用した食事をしているほど,米を食べる機会が少ないということで理解ができます. また,小麦を食べる量が多いほど太っているというのも,炭水化物をたくさん食べるほど太っているということで理解できます. 一方で, 米を食べる量が多いほど痩せているという関係は, あまり自然ではありません.
これは, 一般的に小麦を食べる文化圏の人のほうが,アジア系よりも太っていることに影響されていそうです. yとzの散布図に,xで色をつけることで,xの影響を確認してみましょう.
plt.scatter(y,z,c=x)
plt.xlabel('米の消費量')
plt.ylabel('肥満度')
plt.xlim(-0.1,1.1)
plt.ylim(-0.1,1.1)
plt.grid()
plt.colorbar()
plt.title('ryz='+str(ryz)[:5])
plt.savefig('partial_coeff1.png')
plt.close()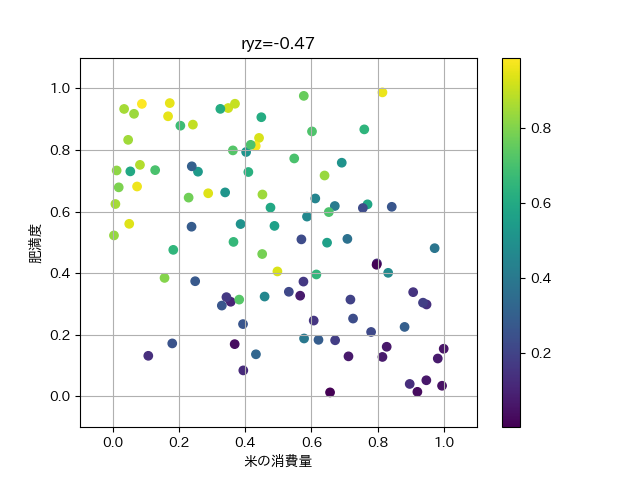
左上に行くほど,xの値を表す色が明るくなっており, xの影響でr_{yz}が負の相関となっていることが分かります.
それでは, 小麦の影響を除いた米の肥満への影響 r_{yz \dor x} を計算してみましょう.
\begin{align*} r_{yz \dot x} &= \frac{r_{yz} - r_{xy}r_xz}{\sqrt{1 - r_{xz}^2}\sqrt{1 - r_{xy}^2}} &\approx \frac{-0.47 + 0.8 \times 0.6}{\sqrt{1 - 0.8^2}\sqrt{1 - 0.6^2}} &\approx 0.02 \end{align*}
Pythonでも計算してみます.
ryzx = (ryz - (rxy * rxz)) / (np.sqrt(1-rxy**2)*np.sqrt(1-rxz**2))
print('ryzx:',ryzx) #0.012866706738387962実際にはほとんど,米の消費量と,肥満度に相関はないことが分かります.
最後に,xの影響を打ち消した,yとzの関係をプロットしてみましょう. これは,この後扱う回帰を利用していますので, コードは理解できなくても問題ありません.
#の影響を除いたyとzの散布図
from sklearn.linear_model import LinearRegression
#yとzのxによる回帰式をたてて,その残渣をプロットすることで,
#xの効果を打ち消したyとzの関係を表現
model_y = LinearRegression().fit(df[['x']], y)
residual_y = y - model_y.predict(df[['x']])
model_z = LinearRegression().fit(df[['x']], z)
residual_z = z - model_z.predict(df[['x']])
(-0.47 + 0.8 * 0.6) / (np.sqrt(1 - 0.8**2) * np.sqrt(1 - 0.6**2))
plt.scatter(residual_z,residual_y,c=x)
plt.xlabel('米の消費量')
plt.ylabel('肥満度')
plt.grid()
plt.colorbar()
plt.title('ryz='+str(ryzx)[:5])
plt.savefig('partial_coeff2.png')
plt.close()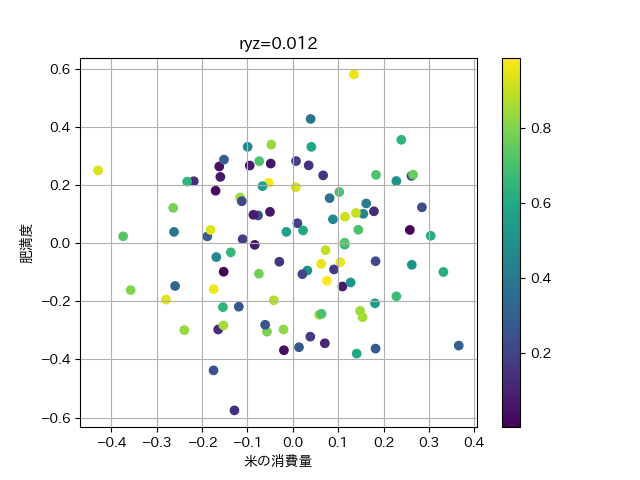
もとのyとzの散布図における,xの広がりの影響が打ち消されて,ほとんど相関がなくなっていることが分かります.
1.5 距離と類似度
ユークリッド距離,コサイン距離